Advertisements
Advertisements
Question
An electric dipole of length 2 cm, when placed with its axis making an angle of 60° with a uniform electric field, experiences a torque of \[8\sqrt{3}\] Nm. Calculate the potential energy of the dipole, if it has a charge \[\pm\] 4 nC.
Solution
Torque, \[\tau = \text { PE sin }\theta = \left( Ql \right)\text { E sin }\theta\] ........ (1)
Here, l is the length of the dipole, Q is the charge and E is the electric field.
Potential energy,
\[\text { U = - P Ecos }\theta = - \left( Ql \right)\text {Ecos}\theta\]
Dividing (2) by (1):
\[\frac{\tau}{U} = \frac{\left( Ql \right)E\sin\theta}{- \left( Ql \right)E\cos\theta} = - \tan\theta\]
\[ \Rightarrow U = - \frac{\tau}{\tan\theta}\]
\[ \Rightarrow U = - \frac{\tau}{\tan {60}^o}\]
\[ \Rightarrow U = - \frac{8\sqrt{3}}{\sqrt{3}}\]
\[ \Rightarrow U = - 8 J\]
APPEARS IN
RELATED QUESTIONS
An electric dipole is placed in an electric field generated by a point charge.
Two particles A and B, of opposite charges 2.0 × 10−6 C and −2.0 × 10−6 C, are placed at a separation of 1.0 cm. Calculate the electric field at a point on the perpendicular bisector of the dipole and 1.0 m away from the centre.
Two-point charges Q1 = 400 μC and Q2 = 100 μC are kept fixed, 60 cm apart in a vacuum. Find the intensity of the electric field at the midpoint of the line joining Q1 and Q2.
Answer the following question.
What is the unit of dipole moment?
Dimensions of mass in electric field and in electric dipole moment are respectively.
An electric dipole is placed at an angle of 30° to a non-uniform electric field. The dipole will experience ________.
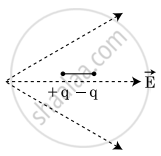
A dipole is placed in an electric field as shown. In which direction will it move?
What work must be done to rotate an electric dipole through an angle θ with the electric field, if an electric dipole of moment p is placed in a uniform electric field E with p parallel to E?
