Advertisements
Advertisements
Question
Two particles A and B, of opposite charges 2.0 × 10−6 C and −2.0 × 10−6 C, are placed at a separation of 1.0 cm. Calculate the electric field at a point on the perpendicular bisector of the dipole and 1.0 m away from the centre.
Solution
Given:
Magnitude of charge, q = 2.0 × 10−6 C
Separation between the charges, l = 1.0 cm
Electric field at at a point on the perpendicular bisector of the dipole,
\[E = \frac{1}{4\pi \epsilon_0}\frac{P}{r '^3}\]
\[E = \frac{9 \times {10}^9 \times 2 \times {10}^{- 8}}{1^3}\]
E = 180 N/C
APPEARS IN
RELATED QUESTIONS
An electric dipole of dipole moment`vecp` consists of point charges +q and −q separated by a distance 2a apart. Deduce the expression for the electric field `vecE` due to the dipole at a distance x from the centre of the dipole on its axial line in terms of the dipole moment `vecp`. Hence show that in the limit x>> a, `vecE->2vecp"/"(4piepsilon_0x^3)`
A system has two charges qA = 2.5 × 10−7 C and qB = −2.5 × 10−7 C located at points A: (0, 0, − 15 cm) and B: (0, 0, + 15 cm), respectively. What are the total charge and electric dipole moment of the system?
Derive the expression for the electric potential due to an electric dipole at a point on its axial line.
Derive an expression for the intensity of electric field at a point in broadside position or on [4)
an equatorial line of an electric dipole.
An electric dipole of length 2 cm, when placed with its axis making an angle of 60° with a uniform electric field, experiences a torque of \[8\sqrt{3}\] Nm. Calculate the potential energy of the dipole, if it has a charge \[\pm\] 4 nC.
Three charges are arranged on the vertices of an equilateral triangle, as shown in the figure. Find the dipole moment of the combination.
Two particles, carrying charges −q and +q and and of mass m each, are fixed at the ends of a light rod of length a to form a dipole. The rod is clamped at an end and is placed in a uniform electric field E with the axis of the dipole along the electric field. The rod is slightly tilted and then released. Neglecting gravity, find the time period of small oscillations.
In an electric dipole, at which point is the electric potential zero ?
An electric dipole consists of two opposite charges each 0.05 µC separated by 30 mm. The dipole is placed in an unifom1 external electric field of 106 NC-1. The maximum torque exerted by the field on the dipole is ______
Dimensions of mass in electric field and in electric dipole moment are respectively.
An electric dipole is placed at an angle of 30° to a non-uniform electric field. The dipole will experience ________.
A conic surface is placed in a uniform electric field E as shown in the figure such that the field is perpendicular to the surface on the side AB. The base of the cone is of radius R, and the height of the cone is h. The angle of the cone is θ.
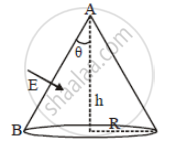
Find the magnitude of the flux that enters the cone's curved surface from the left side. Do not count the outgoing flux (θ < 45°)
An electric dipole of moment p is placed parallel to the uniform electric field. The amount of work done in rotating the dipole by 90° is ____________.
Electric dipole consists of two charges of magnitude 0.1 µC separated by a distance of 2 cm. The dipole is in 5 an external field of 105 N/C. What maximum torque does the field exert on the dipole?
The electric field in a region is given by `vec"E" = 2/5"E"_0hat"i"+3/5"E"_0hat"j"` with `"E"_0 = 4.0xx10^3 "N"/"C"`. The flux of this field through a rectangular surface area 0.4 m2 parallel to the Y - Z plane is ______ Nm2C-1.
A square surface of side l (m) in the plane of the paper. A uniform electric field E(V/m) also in the plane of the paper is limited only to the lower half of the square surface, the electric flux (in SI units) associated with the surface is ______.
Show that intensity of electric field at a point in broadside position of an electric dipole is given by:
E = `(1/(4piepsilon_0)) "p"/(("r"^2 + l^2)^(3//2))`
Where the terms have their usual meaning.
