Advertisements
Advertisements
Question
Two particles, carrying charges −q and +q and and of mass m each, are fixed at the ends of a light rod of length a to form a dipole. The rod is clamped at an end and is placed in a uniform electric field E with the axis of the dipole along the electric field. The rod is slightly tilted and then released. Neglecting gravity, find the time period of small oscillations.
Solution
Consider the rod to be a simple pendulum
Time period of a simple pendulum,
(where l = length and a' = acceleration)
Now
∴ The time period,
APPEARS IN
RELATED QUESTIONS
Depict the orientation of the dipole in (i) stable, (ii) unstable equilibrium in a uniform electric field.
Find the resultant electric field due to an electric dipole of dipole moment, 2aq, (2a being the separation between the charges ±± q) at a point distant 'x' on its equator.
An electric dipole is placed at the centre of a sphere. Mark the correct options.
(a) The flux of the electric field through the sphere is zero.
(b) The electric field is zero at every point of the sphere.
(c) The electric field is not zero anywhere on the sphere.
(d) The electric field is zero on a circle on the sphere.
A sample of HCI gas is placed in an electric field of 2.5 × 104 NC−1. The dipole moment of each HCI molecule is 3.4 × 10−30 Cm. Find the maximum torque that can act on a molecule.
In an electric dipole, at which point is the electric potential zero ?
Answer the following question.
What is the unit of dipole moment?
Dimensions of mass in electric field and in electric dipole moment are respectively.
The electric field at a point on the equatorial plane at a distance r from the centre of a dipole having dipole moment `vec "p"` is given by, (r >> separation of two charges forming the dipole, `epsilon_0 - ` permittivity of free space) ____________.
A conic surface is placed in a uniform electric field E as shown in the figure such that the field is perpendicular to the surface on the side AB. The base of the cone is of radius R, and the height of the cone is h. The angle of the cone is θ.
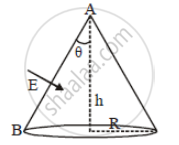
Find the magnitude of the flux that enters the cone's curved surface from the left side. Do not count the outgoing flux (θ < 45°)
An electric dipole of moment p is placed parallel to the uniform electric field. The amount of work done in rotating the dipole by 90° is ____________.
The ratio of the weight of a man in a stationary lift and in a lift accelerating downwards with a uniform acceleration α is 3 : 2. The acceleration of the lift is:
Electric dipole consists of two charges of magnitude 0.1 µC separated by a distance of 2 cm. The dipole is in 5 an external field of 105 N/C. What maximum torque does the field exert on the dipole?
A dipole is placed in an electric field as shown. In which direction will it move?
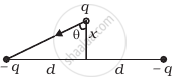
Two charges –q each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced slightly by x(x << d) perpendicular to the line joining the two fixed charged as shown in figure. Show that q will perform simple harmonic oscillation of time period.
`T = [(8pi^3 ε_0 md^3)/q^2]^(1/2)`
The electric potential V as a function of distance X is shown in the figure.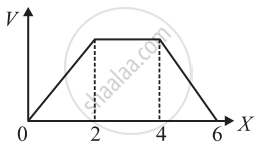
The graph of the magnitude of electric field intensity E as a function of X is ______.
Eight dipoles of charges of magnitude e each are placed inside a cube. The total electric flux coming out of the cube will be ______.
