Advertisements
Advertisements
Question
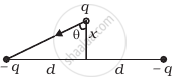
Two charges –q each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced slightly by x(x << d) perpendicular to the line joining the two fixed charged as shown in figure. Show that q will perform simple harmonic oscillation of time period.
`T = [(8pi^3 ε_0 md^3)/q^2]^(1/2)`
Solution
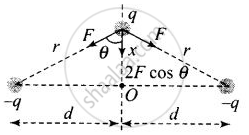
Let the charge q is displaced slightly by x(x << d) perpendicular to the line joining the two fixed charges. Net force on the charge q will be towards O. The motion of charge q to be simple harmonic, if the force on charge q must be proportional to its distance from the centre O and is directed towards O.
Net force on the charge Fnet = 2F cos θ
Here F = `1/(4piε_0) (q(q))/r^2 = 1/(4piε_0) q^2/((d^2 + x^2))`
And cos θ = `x/sqrt(x^2 + d^2)`
Hence, Fnet = `2[1/(4piε_0) q^2/((d^2 + x^2))][x/sqrt(x^2 + d^2)]`
= `1/(2piε_0) (q^2x)/(d^2 + x^2)^(3/2)`
= `1/(2piε_0) (q^2x)/(d^3 (1 + x^2/d^2)^(3/2)`
As x << d, then Fnet = `1/(2piε_0) (q^2x)/d^3` or Fnet = Kx
i.e., force on charge q is proportional to its displacement from the centre O and it is directed towards O. Hence, motion of charge q would be simple harmonic, where ω = `sqrt(K/m)`
And T = `(2pi)/ω = 2pi sqrt(m/K)`
⇒ T = `2pi sqrt((m * 4piε_0 d^3)/(2q^2)) = [(8pi^3ε_0 md^3)/q^2]^(1/2)`
APPEARS IN
RELATED QUESTIONS
Drive the expression for electric field at a point on the equatorial line of an electric dipole.
Three charges are arranged on the vertices of an equilateral triangle, as shown in the figure. Find the dipole moment of the combination.
Answer the following question.
Derive an expression for the electric field at any point on the equatorial line of an electric dipole.
An electric dipole consists of two opposite charges each 0.05 µC separated by 30 mm. The dipole is placed in an unifom1 external electric field of 106 NC-1. The maximum torque exerted by the field on the dipole is ______
An electric dipole is placed at an angle of 30° with an electric field intensity of 2 × 105 N/C. It experiences a torque equal to 4 Nm. The charge on the dipole, if the dipole length is 2 cm, is ______.
When an electric dipole p is placed in a uniform electric field E then at what angle the value of torque will be maximum?
The electric field at a point on the equatorial plane at a distance r from the centre of a dipole having dipole moment `vec "p"` is given by, (r >> separation of two charges forming the dipole, `epsilon_0 - ` permittivity of free space) ____________.
An electric dipole of moment `vec"p"` is placed normal to the lines of force of electric intensity `vec"E"`, then the work done in deflecting it through an angle of 180° is:
Show that intensity of electric field at a point in broadside position of an electric dipole is given by:
E = `(1/(4piepsilon_0)) "p"/(("r"^2 + l^2)^(3//2))`
Where the terms have their usual meaning.
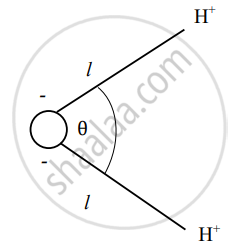
Arrangement of an oxygen ion and two hydrogen ions in a water molecule is shown in figure below.
Calculate electric dipole moment of water molecule. Express your answer in terms of e (charge on hydrogen ion), l and θ.