Advertisements
Advertisements
Question
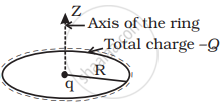
Total charge –Q is uniformly spread along length of a ring of radius R. A small test charge +q of mass m is kept at the centre of the ring and is given a gentle push along the axis of the ring.
- Show that the particle executes a simple harmonic oscillation.
- Obtain its time period.
Solution
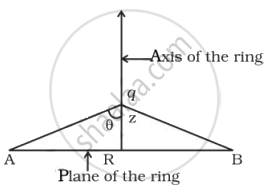
a. Slight push on q along the axis of the ring gives rise to the situation shown in figure. A and B are two points on the ring at the end of a diameter.
Force on q due to line elements `(-Q)/(2piR)` at A and B is
`F_(A + B) = 2 * (-Q)/(2piR) * q * 1/(4piε_0) * 1/r^2 * cos theta`
= `(-Qq)/(piR.4piε_0) * 1/((z^2 + R^2)) * Z/(z^2 + R^2)^(1/2)`
Total force due to ring on q = `(F_(A + B))(piR)`
= `(-Qq)/(4piε_0) z/(z^2 + R^2)^(3/2)`
= `(-Qq)/(4piε_0)` for z << R
Thus, the force is proportional to the negative displacement. Motion under such forces is harmonic.
b. From (a)
`m (d^2z)/(dt^2) = - (Qqz)/(4piε_0R^3)` or `(d^2z)/(dt^2) = - (Qq)/(4piε_0mR^3)z`
That is `ω^2 = (Qq)/(4piε_0mR^3)`. Hence T = `2pisqrt((4piε_0mR)/(Qq))`
APPEARS IN
RELATED QUESTIONS
A conducting sphere of radius 10 cm has an unknown charge. If the electric field 20 cm from the centre of the sphere is 1.5 × 103 N/C and points radially inward, what is the net charge on the sphere?
A proton and an electron are placed in a uniform electric field.
The electric force experienced by a charge of 1.0 × 10−6 C is 1.5 × 10−3 N. Find the magnitude of the electric field at the position of the charge.
A positive charge q is placed in front of a conducting solid cube at a distance d from its centre. Find the electric field at the centre of the cube to the charges appearing on its surface.
A conducting sphere of radius 0.104 m has an unknown charge. If the electric field at 0.20 m from the centre of the sphere is 1.5 x 103 NC-1 and points radially inward, what is the electric flux?
Ionization of a neutral atom is the ______.
Equal charge are given to two-sphere of different radii. The potential will be
A charge of 4 µC is to be divided into two. The distance between the two divided charges is constant. The magnitude of the divided charges so that the force between them is maximum, will be:
Two particles A and B having the same mass have charges +q and +4q, respectively. When they are allowed to fall from rest through the same electric potential difference the ratio of their speeds vA to vB will become ______.
