Advertisements
Advertisements
प्रश्न
Two particles A and B, of opposite charges 2.0 × 10−6 C and −2.0 × 10−6 C, are placed at a separation of 1.0 cm. Calculate the electric field at a point on the perpendicular bisector of the dipole and 1.0 m away from the centre.
उत्तर
Given:
Magnitude of charge, q = 2.0 × 10−6 C
Separation between the charges, l = 1.0 cm
Electric field at at a point on the perpendicular bisector of the dipole,
\[E = \frac{1}{4\pi \epsilon_0}\frac{P}{r '^3}\]
\[E = \frac{9 \times {10}^9 \times 2 \times {10}^{- 8}}{1^3}\]
E = 180 N/C
APPEARS IN
संबंधित प्रश्न
A system has two charges qA = 2.5 × 10−7 C and qB = −2.5 × 10−7 C located at points A: (0, 0, − 15 cm) and B: (0, 0, + 15 cm), respectively. What are the total charge and electric dipole moment of the system?
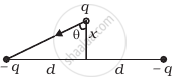
A short electric dipole (which consists of two point charges, +q and -q) is placed at the centre 0 and inside a large cube (ABCDEFGH) of length L, as shown in Figure 1. The electric flux, emanating through the cube is:
a) `q"/"4piin_9L`
b) zero
c) `q"/"2piin_0L`
d) `q"/"3piin_0L`
Derive an expression for the intensity of electric field at a point in broadside position or on [4)
an equatorial line of an electric dipole.
Write the expression for the torque \[\vec{\tau}\] acting on a dipole of dipole moment \[\vec{p}\] placed in an electric field \[\vec{E}\].
Define electric dipole moment. Is it a scalar or a vector? Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
Define electric dipole moment. Write its S.I. unit.
Answer the following question.
What is the unit of dipole moment?
An electric dipole consists of two opposite charges each 0.05 µC separated by 30 mm. The dipole is placed in an unifom1 external electric field of 106 NC-1. The maximum torque exerted by the field on the dipole is ______
When an electric dipole p is placed in a uniform electric field E then at what angle the value of torque will be maximum?
The electric field at a point on the equatorial plane at a distance r from the centre of a dipole having dipole moment `vec "p"` is given by, (r >> separation of two charges forming the dipole, `epsilon_0 - ` permittivity of free space) ____________.
The unit of electric dipole moment is ______.
An electric dipole of moment p is placed parallel to the uniform electric field. The amount of work done in rotating the dipole by 90° is ____________.
The ratio of the weight of a man in a stationary lift and in a lift accelerating downwards with a uniform acceleration α is 3 : 2. The acceleration of the lift is:
Electric dipole consists of two charges of magnitude 0.1 µC separated by a distance of 2 cm. The dipole is in 5 an external field of 105 N/C. What maximum torque does the field exert on the dipole?
A dipole is placed in an electric field as shown. In which direction will it move?
A dipole is placed in an electric field as shown. In which direction will it move?
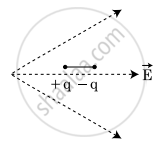
Two charges –q each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced slightly by x(x << d) perpendicular to the line joining the two fixed charged as shown in figure. Show that q will perform simple harmonic oscillation of time period.
`T = [(8pi^3 ε_0 md^3)/q^2]^(1/2)`