Advertisements
Advertisements
Question
Derive the expression for the electric potential due to an electric dipole at a point on its axial line.
Solution
i) Let P be the point at which electric potential is required.
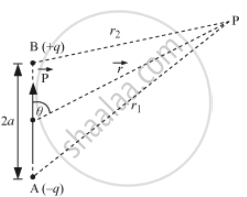
Potential at P due to − q charge,
`V_1=-q/(4piepsilon_0r_1)`
Potential at P due to + q charge,
`V_2=q/(4piepsilon_0r_2)`
Potential at P due to the dipole,
`V=V_1+V_2`
`V=q/(4piepsilon_0)[1/r_2-1/r_1]` .....(i)
Now, by geometry
`r_1^2=r^2+a^2+2arcostheta`
`r_2^2=r^2+a^2+2arcos(180^@-theta)`
`r_2^2=r^2+a^2-2arcostheta`
`r_1^2=r^2(1+a^2/r^2+(2a)/rcostheta)`
If r >> a, `a/r` is small. Therefore,`a^2/r^2` can be neglected.
`r_1^2=r^2(1+(2a)/rcostheta)`
`1/r_1=1/r(1+(2a)/rcostheta)^(1/2)`
similarly, `1/r_2=1/r(1-(2a)/rcostheta)^(1/2)`
Putting these values in (i), we obtain
`V=q/(4piepsilon_0)[1/r(1-(2a)/rcostheta)^(1/2)-1/r(1+(2a)/rcostheta)^(1/2)]`
Using Binomial theorem and retaining terms up to the first order in`a/r`, we obtain
`V=q/(4piepsilon_0r)[1+a/rcostheta-(1-a/rcostheta)]`
`V=q/(4piepsilon_0r)[1+a/rcostheta-1+a/rcostheta]`
`V=q/(4piepsilon_0r)[(2a)/rcostheta]`
`V=(qxx2acostheta)/(4piepsilon_0r^2)`
`V=(Pcostheta)/(4piepsilon_0r^2)`
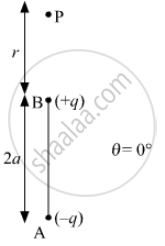
For axial line put θ=0°
`V=(Pcos(0))/(4piepsilon_0r^2)`
`V=P/(4piepsilon_0r^2)`
APPEARS IN
RELATED QUESTIONS
Find the resultant electric field due to an electric dipole of dipole moment, 2aq, (2a being the separation between the charges ±± q) at a point distant 'x' on its equator.
Define dipole moment of an electric dipole. Is it a scalar or a vector?
In which orientation, a dipole placed in a uniform electric field is in (i) stable, (ii) unstable equilibrium?
An electric dipole is placed at the centre of a sphere. Mark the correct options.
(a) The flux of the electric field through the sphere is zero.
(b) The electric field is zero at every point of the sphere.
(c) The electric field is not zero anywhere on the sphere.
(d) The electric field is zero on a circle on the sphere.
Two particles A and B, of opposite charges 2.0 × 10−6 C and −2.0 × 10−6 C, are placed at a separation of 1.0 cm. Two particles A and B, of opposite charges 2.0 × 10−6 C and −2.0 × 10−6 C, are placed at a separation of 1.0 cm.
Answer the following question.
Derive an expression for the electric field at any point on the equatorial line of an electric dipole.
The unit of electric dipole moment is ______.
The electric field in a region is given by `vec"E" = 2/5"E"_0hat"i"+3/5"E"_0hat"j"` with `"E"_0 = 4.0xx10^3 "N"/"C"`. The flux of this field through a rectangular surface area 0.4 m2 parallel to the Y - Z plane is ______ Nm2C-1.
