Advertisements
Advertisements
Question
A electron of mass me revolves around a nucleus of charge +Ze. Show that it behaves like a tiny magnetic dipole. Hence prove that the magnetic moment associated wit it is expressed as `vecμ =−e/(2 m_e)vecL `, where `vec L` is the orbital angular momentum of the electron. Give the significance of negative sign.
Solution 1
Electrons revolve around the nucleus. A revolving electron is like a loop of current. which has a definite dipole moment.When electron revolves in anticlockwise direction, the equivalent current is clockwise. Therefore, upper face of the electron loop acts as south pole and lower face acts as north pole. Hence, an atom behaves as a magnetic dipole.
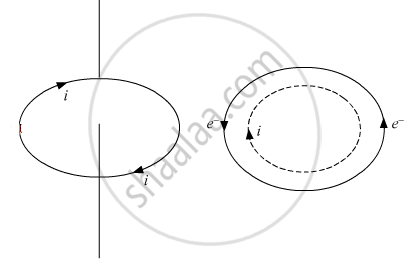
If e is the charge on an electron revolving in an orbit of radius r with a uniform angular velocity ω, then equivalent current `i="charge"/"time"=e/T`
T=the period of revolution of electron
`i=e/((2π)/ω)=(ωe)/(2π)`
`A=πr^2`
magnetic moment of the atom is given by
`μ=iA=(ωe)/(2π)πr^2`
`μ=1/2eω^2`
According to Bohr's theory
`mvr=(nh)/(2π)` where n=1,2,3.... denotes the number of the orbit.
`v=rω`
`m(rω)r=(nh)/(2π)`
`ωr^2=(nh)/(2πm_e)`
`vecμ =1/2 e nh/(2πme)`
`vecmu=n(eh)/(4πm_e) (vecL=(nh)/(2π))`
`μ⃗ =−e/(2m_e)vecL`
The negative sign has been included for the reason that electron has negative charge.
Solution 2
Electrons revolve around the nucleus. A revolving electron is like a loop of current. which has a definite dipole moment.When electron revolves in anticlockwise direction, the equivalent current is clockwise. Therefore, upper face of the electron loop acts as south pole and lower face acts as north pole. Hence, an atom behaves as a magnetic dipole.

If e is the charge on an electron revolving in an orbit of radius r with a uniform angular velocity ω, then equivalent current `i="charge"/"time"=e/T`
T=the period of revolution of electron
`i=e/((2π)/ω)=(ωe)/(2π)`
`A=πr^2`
magnetic moment of the atom is given by
`μ=iA=(ωe)/(2π)πr^2`
`μ=1/2eω^2`
According to Bohr's theory
`mvr=(nh)/(2π)` where n=1,2,3.... denotes the number of the orbit.
`v=rω`
`m(rω)r=(nh)/(2π)`
`ωr^2=(nh)/(2πm_e)`
`vecμ =1/2 e nh/(2πme)`
`vecmu=n(eh)/(4πm_e) (vecL=(nh)/(2π))`
`μ⃗ =−e/(2m_e)vecL`
The negative sign has been included for the reason that electron has negative charge.
APPEARS IN
RELATED QUESTIONS
For what kinetic energy of a neutron will the associated de Broglie wavelength be 1.40 × 10−10 m?
Find the de Broglie wavelength of a neutron, in thermal equilibrium with matter, having an average kinetic energy of `(3/2)` kT at 300 K.
Crystal diffraction experiments can be performed using X-rays, or electrons accelerated through appropriate voltage. Which probe has greater energy? (For quantitative comparison, take the wavelength of the probe equal to 1 Å, which is of the order of inter-atomic spacing in the lattice) (me = 9.11 × 10−31 kg).
Obtain the de Broglie wavelength of a neutron of kinetic energy 150 eV. As you have an electron beam of this energy is suitable for crystal diffraction experiments. Would a neutron beam of the same energy be equally suitable? Explain. (mn= 1.675 × 10−27 kg)
The wavelength λ of a photon and the de-Broglie wavelength of an electron have the same value. Show that energy of a photon in (2λmc/h) times the kinetic energy of electron; where m, c and h have their usual meaning.
Relativistic corrections become necessary when the expression for the kinetic energy `1/2 mv^2`, becomes comparable with mc2, where m is the mass of the particle. At what de Broglie wavelength will relativistic corrections become important for an electron?
- λ = 10 nm
- λ = 10–1 nm
- λ = 10–4 nm
- λ = 10–6 nm
A proton and an α-particle are accelerated, using the same potential difference. How are the de-Broglie wavelengths λp and λa related to each other?
The equation λ = `1.227/"x"` nm can be used to find the de Brogli wavelength of an electron. In this equation x stands for:
Where,
m = mass of electron
P = momentum of electron
K = Kinetic energy of electron
V = Accelerating potential in volts for electron
For which of the following particles will it be most difficult to experimentally verify the de-Broglie relationship?
How will the de-Broglie wavelength associated with an electron be affected when the velocity of the electron decreases? Justify your answer.
