Advertisements
Advertisements
प्रश्न
A electron of mass me revolves around a nucleus of charge +Ze. Show that it behaves like a tiny magnetic dipole. Hence prove that the magnetic moment associated wit it is expressed as `vecμ =−e/(2 m_e)vecL `, where `vec L` is the orbital angular momentum of the electron. Give the significance of negative sign.
Advertisements
उत्तर १
Electrons revolve around the nucleus. A revolving electron is like a loop of current. which has a definite dipole moment.When electron revolves in anticlockwise direction, the equivalent current is clockwise. Therefore, upper face of the electron loop acts as south pole and lower face acts as north pole. Hence, an atom behaves as a magnetic dipole.
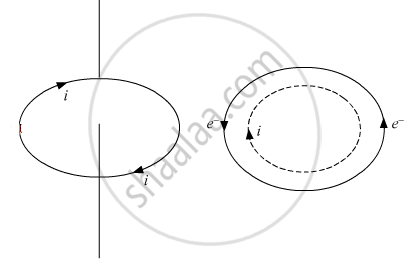
If e is the charge on an electron revolving in an orbit of radius r with a uniform angular velocity ω, then equivalent current `i="charge"/"time"=e/T`
T=the period of revolution of electron
`i=e/((2π)/ω)=(ωe)/(2π)`
`A=πr^2`
magnetic moment of the atom is given by
`μ=iA=(ωe)/(2π)πr^2`
`μ=1/2eω^2`
According to Bohr's theory
`mvr=(nh)/(2π)` where n=1,2,3.... denotes the number of the orbit.
`v=rω`
`m(rω)r=(nh)/(2π)`
`ωr^2=(nh)/(2πm_e)`
`vecμ =1/2 e nh/(2πme)`
`vecmu=n(eh)/(4πm_e) (vecL=(nh)/(2π))`
`μ⃗ =−e/(2m_e)vecL`
The negative sign has been included for the reason that electron has negative charge.
उत्तर २
Electrons revolve around the nucleus. A revolving electron is like a loop of current. which has a definite dipole moment.When electron revolves in anticlockwise direction, the equivalent current is clockwise. Therefore, upper face of the electron loop acts as south pole and lower face acts as north pole. Hence, an atom behaves as a magnetic dipole.
If e is the charge on an electron revolving in an orbit of radius r with a uniform angular velocity ω, then equivalent current `i="charge"/"time"=e/T`
T=the period of revolution of electron
`i=e/((2π)/ω)=(ωe)/(2π)`
`A=πr^2`
magnetic moment of the atom is given by
`μ=iA=(ωe)/(2π)πr^2`
`μ=1/2eω^2`
According to Bohr's theory
`mvr=(nh)/(2π)` where n=1,2,3.... denotes the number of the orbit.
`v=rω`
`m(rω)r=(nh)/(2π)`
`ωr^2=(nh)/(2πm_e)`
`vecμ =1/2 e nh/(2πme)`
`vecmu=n(eh)/(4πm_e) (vecL=(nh)/(2π))`
`μ⃗ =−e/(2m_e)vecL`
The negative sign has been included for the reason that electron has negative charge.
APPEARS IN
संबंधित प्रश्न
What is the
(a) momentum,
(b) speed, and
(c) de Broglie wavelength of an electron with kinetic energy of 120 eV.
The wavelength of light from the spectral emission line of sodium is 589 nm. Find the kinetic energy at which
(a) an electron, and
(b) a neutron, would have the same de Broglie wavelength.
For what kinetic energy of a neutron will the associated de Broglie wavelength be 1.40 × 10−10 m?
What is the de Broglie wavelength of a nitrogen molecule in air at 300 K? Assume that the molecule is moving with the root-mean square speed of molecules at this temperature. (Atomic mass of nitrogen = 14.0076 u)
A proton and an α-particle are accelerated, using the same potential difference. How are the de-Broglie wavelengths λp and λa related to each other?
Two particles move at a right angle to each other. Their de-Broglie wavelengths are λ1 and λ2 respectively. The particles suffer a perfectly inelastic collision. The de-Broglie wavelength λ, of the final particle, is given by ______.
The De-Broglie wavelength of electron in the third Bohr orbit of hydrogen is ______ × 10-11 m (given radius of first Bohr orbit is 5.3 × 10-11 m):
An electron of mass me, and a proton of mass mp = 1836 me are moving with the same speed. The ratio of the de Broglie wavelength `lambda_"electron"/lambda_"proton"` will be:
In a Frank-Hertz experiment, an electron of energy 5.6 eV passes through mercury vapour and emerges with an energy 0.7 eV. The minimum wavelength of photons emitted by mercury atoms is close to ______.
How will the de-Broglie wavelength associated with an electron be affected when the accelerating potential is increased? Justify your answer.
