Advertisements
Advertisements
प्रश्न
A electron of mass me revolves around a nucleus of charge +Ze. Show that it behaves like a tiny magnetic dipole. Hence prove that the magnetic moment associated wit it is expressed as `vecμ =−e/(2 m_e)vecL `, where `vec L` is the orbital angular momentum of the electron. Give the significance of negative sign.
उत्तर १
Electrons revolve around the nucleus. A revolving electron is like a loop of current. which has a definite dipole moment.When electron revolves in anticlockwise direction, the equivalent current is clockwise. Therefore, upper face of the electron loop acts as south pole and lower face acts as north pole. Hence, an atom behaves as a magnetic dipole.
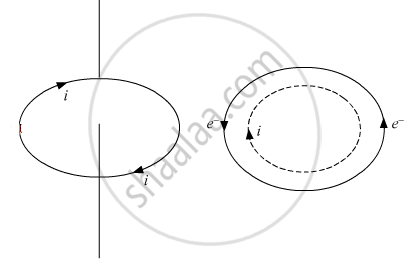
If e is the charge on an electron revolving in an orbit of radius r with a uniform angular velocity ω, then equivalent current `i="charge"/"time"=e/T`
T=the period of revolution of electron
`i=e/((2π)/ω)=(ωe)/(2π)`
`A=πr^2`
magnetic moment of the atom is given by
`μ=iA=(ωe)/(2π)πr^2`
`μ=1/2eω^2`
According to Bohr's theory
`mvr=(nh)/(2π)` where n=1,2,3.... denotes the number of the orbit.
`v=rω`
`m(rω)r=(nh)/(2π)`
`ωr^2=(nh)/(2πm_e)`
`vecμ =1/2 e nh/(2πme)`
`vecmu=n(eh)/(4πm_e) (vecL=(nh)/(2π))`
`μ⃗ =−e/(2m_e)vecL`
The negative sign has been included for the reason that electron has negative charge.
उत्तर २
Electrons revolve around the nucleus. A revolving electron is like a loop of current. which has a definite dipole moment.When electron revolves in anticlockwise direction, the equivalent current is clockwise. Therefore, upper face of the electron loop acts as south pole and lower face acts as north pole. Hence, an atom behaves as a magnetic dipole.

If e is the charge on an electron revolving in an orbit of radius r with a uniform angular velocity ω, then equivalent current `i="charge"/"time"=e/T`
T=the period of revolution of electron
`i=e/((2π)/ω)=(ωe)/(2π)`
`A=πr^2`
magnetic moment of the atom is given by
`μ=iA=(ωe)/(2π)πr^2`
`μ=1/2eω^2`
According to Bohr's theory
`mvr=(nh)/(2π)` where n=1,2,3.... denotes the number of the orbit.
`v=rω`
`m(rω)r=(nh)/(2π)`
`ωr^2=(nh)/(2πm_e)`
`vecμ =1/2 e nh/(2πme)`
`vecmu=n(eh)/(4πm_e) (vecL=(nh)/(2π))`
`μ⃗ =−e/(2m_e)vecL`
The negative sign has been included for the reason that electron has negative charge.
APPEARS IN
संबंधित प्रश्न
What is the de Broglie wavelength of a ball of mass 0.060 kg moving at a speed of 1.0 m/s?
Find the de Broglie wavelength of a neutron, in thermal equilibrium with matter, having an average kinetic energy of `(3/2)` kT at 300 K.
Describe briefly how the Davisson-Germer experiment demonstrated the wave nature of electrons.
Sodium and copper have work function 2.3 eV and 4.5 eV respectively. Then, the ratio of the wavelengths is nearest to ______.
A proton and α-particle are accelerated through the same potential difference. The ratio of the de-Broglie wavelength λp to that λα is _______.
Given below are two statements:
Statement - I: Two photons having equal linear momenta have equal wavelengths.
Statement - II: If the wavelength of photon is decreased, then the momentum and energy of a photon will also decrease.
In the light of the above statements, choose the correct answer from the options given below.
The equation λ = `1.227/"x"` nm can be used to find the de Brogli wavelength of an electron. In this equation x stands for:
Where,
m = mass of electron
P = momentum of electron
K = Kinetic energy of electron
V = Accelerating potential in volts for electron
An electron of mass me, and a proton of mass mp = 1836 me are moving with the same speed. The ratio of the de Broglie wavelength `lambda_"electron"/lambda_"proton"` will be:
In a Frank-Hertz experiment, an electron of energy 5.6 eV passes through mercury vapour and emerges with an energy 0.7 eV. The minimum wavelength of photons emitted by mercury atoms is close to ______.
How will the de-Broglie wavelength associated with an electron be affected when the velocity of the electron decreases? Justify your answer.
