Advertisements
Advertisements
प्रश्न
Derive the expression for the electric potential due to an electric dipole at a point on its axial line.
उत्तर
i) Let P be the point at which electric potential is required.
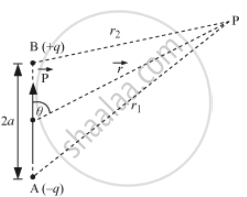
Potential at P due to − q charge,
`V_1=-q/(4piepsilon_0r_1)`
Potential at P due to + q charge,
`V_2=q/(4piepsilon_0r_2)`
Potential at P due to the dipole,
`V=V_1+V_2`
`V=q/(4piepsilon_0)[1/r_2-1/r_1]` .....(i)
Now, by geometry
`r_1^2=r^2+a^2+2arcostheta`
`r_2^2=r^2+a^2+2arcos(180^@-theta)`
`r_2^2=r^2+a^2-2arcostheta`
`r_1^2=r^2(1+a^2/r^2+(2a)/rcostheta)`
If r >> a, `a/r` is small. Therefore,`a^2/r^2` can be neglected.
`r_1^2=r^2(1+(2a)/rcostheta)`
`1/r_1=1/r(1+(2a)/rcostheta)^(1/2)`
similarly, `1/r_2=1/r(1-(2a)/rcostheta)^(1/2)`
Putting these values in (i), we obtain
`V=q/(4piepsilon_0)[1/r(1-(2a)/rcostheta)^(1/2)-1/r(1+(2a)/rcostheta)^(1/2)]`
Using Binomial theorem and retaining terms up to the first order in`a/r`, we obtain
`V=q/(4piepsilon_0r)[1+a/rcostheta-(1-a/rcostheta)]`
`V=q/(4piepsilon_0r)[1+a/rcostheta-1+a/rcostheta]`
`V=q/(4piepsilon_0r)[(2a)/rcostheta]`
`V=(qxx2acostheta)/(4piepsilon_0r^2)`
`V=(Pcostheta)/(4piepsilon_0r^2)`
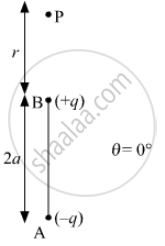
For axial line put θ=0°
`V=(Pcos(0))/(4piepsilon_0r^2)`
`V=P/(4piepsilon_0r^2)`
APPEARS IN
संबंधित प्रश्न
Define dipole moment of an electric dipole. Is it a scalar or a vector?
A sample of HCI gas is placed in an electric field of 2.5 × 104 NC−1. The dipole moment of each HCI molecule is 3.4 × 10−30 Cm. Find the maximum torque that can act on a molecule.
In an electric dipole, at which point is the electric potential zero ?
A conic surface is placed in a uniform electric field E as shown in the figure such that the field is perpendicular to the surface on the side AB. The base of the cone is of radius R, and the height of the cone is h. The angle of the cone is θ.
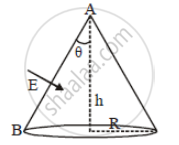
Find the magnitude of the flux that enters the cone's curved surface from the left side. Do not count the outgoing flux (θ < 45°)
An electric dipole of moment `vec"p"` is placed normal to the lines of force of electric intensity `vec"E"`, then the work done in deflecting it through an angle of 180° is:
Polar molecules are the molecules ______.
The electric potential V as a function of distance X is shown in the figure.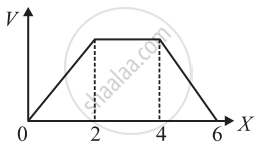
The graph of the magnitude of electric field intensity E as a function of X is ______.
The electric field in a region is given by `vec"E" = 2/5"E"_0hat"i"+3/5"E"_0hat"j"` with `"E"_0 = 4.0xx10^3 "N"/"C"`. The flux of this field through a rectangular surface area 0.4 m2 parallel to the Y - Z plane is ______ Nm2C-1.
In an electric dipole, what is the locus of a point having zero potential?
