Advertisements
Advertisements
प्रश्न
Derive the expression for the electric potential due to an electric dipole at a point on its axial line.
उत्तर
i) Let P be the point at which electric potential is required.
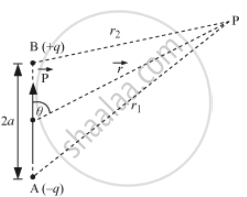
Potential at P due to − q charge,
`V_1=-q/(4piepsilon_0r_1)`
Potential at P due to + q charge,
`V_2=q/(4piepsilon_0r_2)`
Potential at P due to the dipole,
`V=V_1+V_2`
`V=q/(4piepsilon_0)[1/r_2-1/r_1]` .....(i)
Now, by geometry
`r_1^2=r^2+a^2+2arcostheta`
`r_2^2=r^2+a^2+2arcos(180^@-theta)`
`r_2^2=r^2+a^2-2arcostheta`
`r_1^2=r^2(1+a^2/r^2+(2a)/rcostheta)`
If r >> a, `a/r` is small. Therefore,`a^2/r^2` can be neglected.
`r_1^2=r^2(1+(2a)/rcostheta)`
`1/r_1=1/r(1+(2a)/rcostheta)^(1/2)`
similarly, `1/r_2=1/r(1-(2a)/rcostheta)^(1/2)`
Putting these values in (i), we obtain
`V=q/(4piepsilon_0)[1/r(1-(2a)/rcostheta)^(1/2)-1/r(1+(2a)/rcostheta)^(1/2)]`
Using Binomial theorem and retaining terms up to the first order in`a/r`, we obtain
`V=q/(4piepsilon_0r)[1+a/rcostheta-(1-a/rcostheta)]`
`V=q/(4piepsilon_0r)[1+a/rcostheta-1+a/rcostheta]`
`V=q/(4piepsilon_0r)[(2a)/rcostheta]`
`V=(qxx2acostheta)/(4piepsilon_0r^2)`
`V=(Pcostheta)/(4piepsilon_0r^2)`
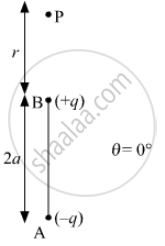
For axial line put θ=0°
`V=(Pcos(0))/(4piepsilon_0r^2)`
`V=P/(4piepsilon_0r^2)`
APPEARS IN
संबंधित प्रश्न
An electric dipole of length 4 cm, when placed with its axis making an angle of 60° with a uniform electric field, experiences a torque of `4sqrt3`Nm. Calculate the potential energy of the dipole, if it has charge ±8 nC
An electric dipole is placed at the centre of a sphere. Mark the correct options.
(a) The flux of the electric field through the sphere is zero.
(b) The electric field is zero at every point of the sphere.
(c) The electric field is not zero anywhere on the sphere.
(d) The electric field is zero on a circle on the sphere.
Two particles A and B, of opposite charges 2.0 × 10−6 C and −2.0 × 10−6 C, are placed at a separation of 1.0 cm. Two particles A and B, of opposite charges 2.0 × 10−6 C and −2.0 × 10−6 C, are placed at a separation of 1.0 cm.
On the axis and on the equator of an electric dipole for all points ____________.
Electric field on the axis of a small electric dipole at a distance r is E1 and at a distance of 2r on its perpendicular bisector, the electric field is E2. Then the ratio E2: E1 is ______.
Electric charges q, q, - 2q are placed at the comers of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is ____________.
The ratio of the weight of a man in a stationary lift and in a lift accelerating downwards with a uniform acceleration α is 3 : 2. The acceleration of the lift is:
In a non-uniform electric field, electric dipole experiences:-
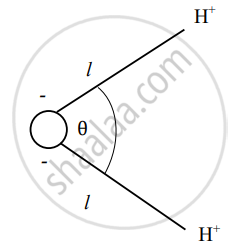
Arrangement of an oxygen ion and two hydrogen ions in a water molecule is shown in figure below.
Calculate electric dipole moment of water molecule. Express your answer in terms of e (charge on hydrogen ion), l and θ.