Advertisements
Advertisements
Question
Eight identical cells, each of emf 2V and internal resistance 3 Ω, are connected in series to form a row. Six such rows are connected in parallel to form a battery. This battery is now connected to an external resistor R of resistance 6 Ω. Calculate:
- emf of the battery.
- internal resistance of the battery.
- current flowing through R.
Solution
- The emf of each cell is 2 V, and there are 8 cells connected in series. Therefore the emf of the battery is 2 V × 8 = 16 V.
- When cells are connected in series, the total internal resistance is the sum of all the internal resistances of each cell.
Since there are 8 cells, the total internal resistance is 3 Ω × 8 = 24 Ω.
The formula provides the total internal resistance when connecting cells in parallel.
`therefore 1/"R" = 1/"R"_1 + 1/"R"_2 + 1/"R"_3 + ... + 1/"R"_"L"`
`therefore 1/"R" = 1/24 + ... + 1/24` (6 times)
⇒ R = 4 Ω
Thus, the internal resistance of the battery is 4 Ω. - To calculate the current flowing through the external resistance R, we need to first calculate the total resistance of the circuit.
The external resistance has a resistance of 6 Ω and the internal resistance of the battery is 4 Ω.
When the resistors are connected in series, the total resistance is the sum of the individual resistance.
∴ Rtotal = 6 + 4 = 10 Ω
From ohm's law
I = `"V"/"R" = 16/10 = 1.6` A
Therefore, the current flowing through the external resistor R is 1.6 A.
APPEARS IN
RELATED QUESTIONS
Three resistors 2 Ω, 4 Ω and 5 Ω are combined in parallel. What is the total resistance of the combination?
Suppose you have three resistors, each of value 30 Ω. List all the different resistances you can obtain using them.
Which of the following quantities does not change when a resistor connected to a battery is heated due to the current?
An ideal battery sends a current of 5 A in a resistor. When another resistor of 10 Ω is connected in parallel, the current through the battery is increased to 6 A. Find the resistance of the first resistor.
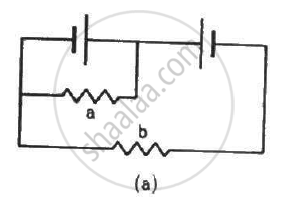
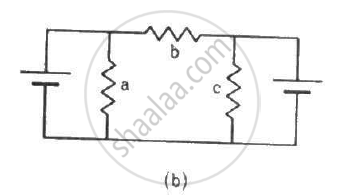
Each of the resistors shown in the figure has a resistance of 10 Ω and each of the batteries has an emf of 10 V. Find the currents flowing through the resistors a and bin the two circuits.
The emf ε and the internal resistance r of the battery, shown in the figure, are 4.3 V and 1.0 Ω respectively. The external resistance R is 50 Ω. The resistances of the ammeter and voltmeter are 2.0 Ω and 200 Ω respectively. (a) Find the readings of the two meters. (b) The switch is thrown to the other side. What will be the readings of the two meters now?

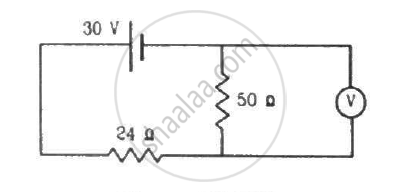
The voltmeter shown in the figure reads 18 V across the 50 Ω resistor. Find the resistance of the voltmeter.
If the combination is connected to a battery of emf 20 V and negligible internal resistance, determine the current through each resistor, and the total current drawn from the battery.
The instantaneous values of emf and the current in a series ac circuit are-
E = Eo Sin ωt and I = Io sin (ωt+π/3) respectively, then it is ______.
A condenses having a capacity 2.0 µF is charged to 200 V and the plates of the capacitor are connected to a resistance wire. The heat produce in it will be:-
