Advertisements
Advertisements
Question
The emf ε and the internal resistance r of the battery, shown in the figure, are 4.3 V and 1.0 Ω respectively. The external resistance R is 50 Ω. The resistances of the ammeter and voltmeter are 2.0 Ω and 200 Ω respectively. (a) Find the readings of the two meters. (b) The switch is thrown to the other side. What will be the readings of the two meters now?

Solution
(a)
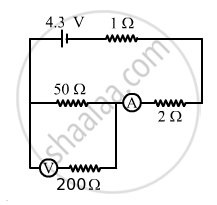
The 50 Ω and 200 Ω resistances are in parallel. Their equivalent resistance,
\[R_{eqv} = \frac{50 \times 200}{50 + 200} = 40 \Omega\]
This equivalent resistance and the 2 Ω and 1 Ω resistances are connected in series. The effective resistance of the circuit,
\[R_{eff} = \left( 40 + 2 + 1 \right) = 43 \Omega\]
In this case, the ammeter will read the total current of the circuit. The current through the ammeter,
\[i = \frac{4 . 3}{43} = 0 . 1 A\]
This current will be distributed in the inverse ratio of resistance between the resistances 50 Ω and 200 Ω. The current through the voltmeter,
\[i' = \frac{50}{\left( 50 + 200 \right)}i\]
\[ \Rightarrow i' = 0 . 02 A\]
Reading of the voltmeter = 0.02 × 200 = 4 V
(b)
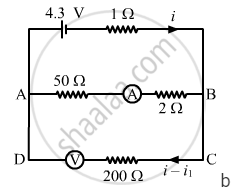
The two branches AB and CD are in parallel. Their equivalent resistance,
\[R_{eqv} = \frac{52 \times 200}{52 + 200} = 41 . 27 A\]
This equivalent resistance is in series with the 1 Ω resistance. The effective resistance of the circuit,
\[R_{eff} = \left( 41 . 27 + 1 \right) \Omega = 42 . 27 \Omega\]
The total current through the circuit,
\[i = \frac{4 . 3}{42 . 27} = 0 . 1 A\]
In this case, the ammeter will read the current flowing through the 50 Ω resistance, which is i1, as shown. The currents in the two parallel branches will distribute in the inverse ratio of the resistances.
\[\therefore i_1 = \left( \frac{200}{200 + 52} \right)i\]
\[ \Rightarrow i_i = 0 . 08 A\]
The current through the voltmeter = i - i1 = 0.02 A
The reading of the voltmeter = 0.02 × 200 = 4 V
APPEARS IN
RELATED QUESTIONS
Three resistors 1 Ω, 2 Ω, and 3 Ω are combined in series. What is the total resistance of the combination?
If the combination is connected to a battery of emf 12 V and negligible internal resistance, obtain the potential drop across each resistor.
Two resistors R1 = 400Ω and R2 = 20 n are connected in parallel to a battery. If heating the power developed in R1 is 25 W. find the heating power developed in R2
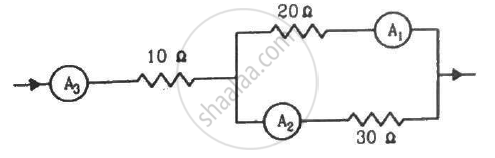
If the reading of the ammeter, A1 in the following figure is 2.4 A, what will be the readings of ammeters A2 and A3? Neglect the resistances of the ammeters.
An ideal battery sends a current of 5 A in a resistor. When another resistor of 10 Ω is connected in parallel, the current through the battery is increased to 6 A. Find the resistance of the first resistor.
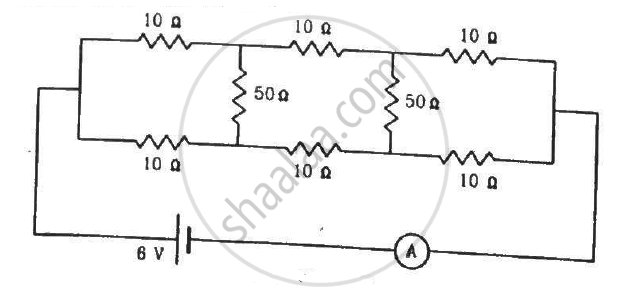
Find the current measured by the ammeter in the circuit shown in the figure.
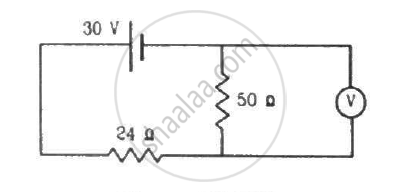
The voltmeter shown in the figure reads 18 V across the 50 Ω resistor. Find the resistance of the voltmeter.
A voltmeter coil has resistance 50.0 Ω and a resistor of 1.15 kΩ is connected in series. It can read potential differences up to 12 volts. If this same coil is used to construct an ammeter that can measure currents up to 2.0 A, what should be the resistance of the shunt used?
Two voltameters, one with a solution of silver salt and the other with a trivalent-metal salt, are connected in series and a current of 2 A is maintained for 1.50 hours. It is found that 1.00 g of the trivalent metal is deposited. (a) What is the atomic weight of the trivalent metal?
(b) How much silver is deposited during this period? Atomic weight of silver is 107.9 g mol−1.
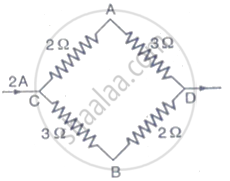
A current of 2 A flows in conductors as shown. The potential difference VA- VB will be ________.
An electric current is passed through a circuit containing two wires of the same material, connected in parallel. If the lengths and radii of the wires are in the ratio of 3:2 and 2:3, then the ratio of the current passing through the wire will be ____________.
Three resistors having values R battery. Suppose R1 carries a current of 2.0 A, R ohms, and R3 dissipates 6.0 watts of power. Then the voltage across R is ______.
The effective resistance of a parallel connection that consists of four wires of equal length, equal area of cross-section and same material is 0.25 Ω. What will be the effective resistance if they are connected in series?
Let there be n resistors R1............Rn with Rmax = max (R1......... Rn) and Rmin = min {R1..... Rn}. Show that when they are connected in parallel, the resultant resistance RP < R min and when they are connected in series, the resultant resistance RS > Rmax. Interpret the result physically.
An electric cable of copper has just one wire of radius 9 mm. Its resistance is 14Ω. If this single copper wire of the cable is replaced by seven identical well insulated copper wires each of radius 3 mm connected in parallel, then the new resistance of the combination will be:
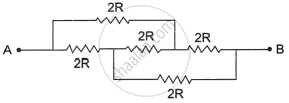
- Assertion (A): The equivalent resistance between points A and B in the given networks is 2R.
- Reason (R): All the resistors are connected in parallel.
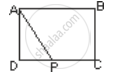
A wire of uniform cross-section and resistance 4 ohms is bent in the shape of square ABCD. Point A is connected to point P on DC by a wire AP of resistance 1 ohm. When a potential difference is applied between A and C, the points B and P are seen to be at the same potential. What is the resistance of the part DP?