Advertisements
Advertisements
प्रश्न
The emf ε and the internal resistance r of the battery, shown in the figure, are 4.3 V and 1.0 Ω respectively. The external resistance R is 50 Ω. The resistances of the ammeter and voltmeter are 2.0 Ω and 200 Ω respectively. (a) Find the readings of the two meters. (b) The switch is thrown to the other side. What will be the readings of the two meters now?

उत्तर
(a)
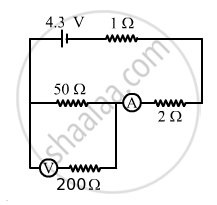
The 50 Ω and 200 Ω resistances are in parallel. Their equivalent resistance,
\[R_{eqv} = \frac{50 \times 200}{50 + 200} = 40 \Omega\]
This equivalent resistance and the 2 Ω and 1 Ω resistances are connected in series. The effective resistance of the circuit,
\[R_{eff} = \left( 40 + 2 + 1 \right) = 43 \Omega\]
In this case, the ammeter will read the total current of the circuit. The current through the ammeter,
\[i = \frac{4 . 3}{43} = 0 . 1 A\]
This current will be distributed in the inverse ratio of resistance between the resistances 50 Ω and 200 Ω. The current through the voltmeter,
\[i' = \frac{50}{\left( 50 + 200 \right)}i\]
\[ \Rightarrow i' = 0 . 02 A\]
Reading of the voltmeter = 0.02 × 200 = 4 V
(b)
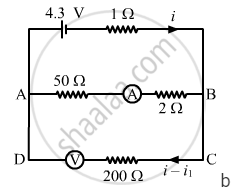
The two branches AB and CD are in parallel. Their equivalent resistance,
\[R_{eqv} = \frac{52 \times 200}{52 + 200} = 41 . 27 A\]
This equivalent resistance is in series with the 1 Ω resistance. The effective resistance of the circuit,
\[R_{eff} = \left( 41 . 27 + 1 \right) \Omega = 42 . 27 \Omega\]
The total current through the circuit,
\[i = \frac{4 . 3}{42 . 27} = 0 . 1 A\]
In this case, the ammeter will read the current flowing through the 50 Ω resistance, which is i1, as shown. The currents in the two parallel branches will distribute in the inverse ratio of the resistances.
\[\therefore i_1 = \left( \frac{200}{200 + 52} \right)i\]
\[ \Rightarrow i_i = 0 . 08 A\]
The current through the voltmeter = i - i1 = 0.02 A
The reading of the voltmeter = 0.02 × 200 = 4 V
APPEARS IN
संबंधित प्रश्न
Three resistors 1 Ω, 2 Ω, and 3 Ω are combined in series. What is the total resistance of the combination?
If the combination is connected to a battery of emf 12 V and negligible internal resistance, obtain the potential drop across each resistor.
Three identical cells each of emf 2V and internal resistance 10 Ω are connected in series to form a battery. The battery is then connected to a parallel combination of two identical resistors, each of resistance 6 Ω. Find the current delivered by the battery.
Which of the following quantities does not change when a resistor connected to a battery is heated due to the current?
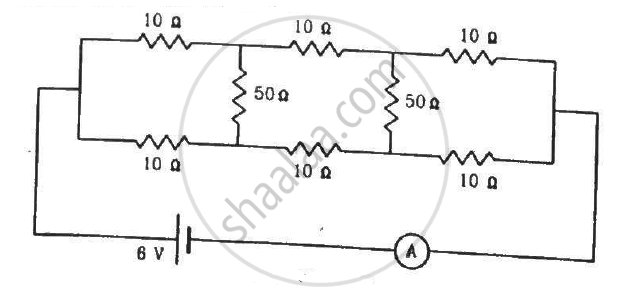
Find the current measured by the ammeter in the circuit shown in the figure.
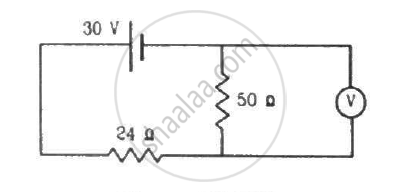
The voltmeter shown in the figure reads 18 V across the 50 Ω resistor. Find the resistance of the voltmeter.
A solenoid L and a resistor R are connected in series to a battery, through a switch. When the switch is put on, current I flowing through it varies with time t as shown in which of the graphs given below:
If the combination is connected to a battery of emf 20 V and negligible internal resistance, determine the current through each resistor, and the total current drawn from the battery.
To get maximum current in a resistance of 3 ohms, one can use n rows of m cells (connected in series) connected in parallel. If the total number of cells is 24 and the internal resistance of a cell is 0.5 ohms then ______.
In parallel combination of n cells, we obtain ______.
If two resistors of resistances R1 = (4 ± 0.5) Ω and R2 = (16 ± 0.5) Ω are connected in series. The eqivalent resistance with the limits of percentage error is ______.
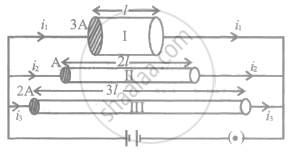
The figure shows three conductors I, II and III of same material, different lengths l, 2l and 3l and of different areas of cross-sections 3A, A and 2A respectively. Arrange them in the increasing order of current drawn from the battery.
How many times will the resistance of an identical conductor be increase, if the parallel resistance be change to series one?
The effective resistance of a parallel connection that consists of four wires of equal length, equal area of cross-section and same material is 0.25 Ω. What will be the effective resistance if they are connected in series?
An electric cable of copper has just one wire of radius 9 mm. Its resistance is 14Ω. If this single copper wire of the cable is replaced by seven identical well insulated copper wires each of radius 3 mm connected in parallel, then the new resistance of the combination will be:
Three bulbs B1 (230V, 40W), B2 (230V, 60W) and B3 (230V, 100W) are connected in series to a 230V supply. Which bulb glows the brightest?
