Advertisements
Advertisements
प्रश्न
Eight identical cells, each of emf 2V and internal resistance 3 Ω, are connected in series to form a row. Six such rows are connected in parallel to form a battery. This battery is now connected to an external resistor R of resistance 6 Ω. Calculate:
- emf of the battery.
- internal resistance of the battery.
- current flowing through R.
उत्तर
- The emf of each cell is 2 V, and there are 8 cells connected in series. Therefore the emf of the battery is 2 V × 8 = 16 V.
- When cells are connected in series, the total internal resistance is the sum of all the internal resistances of each cell.
Since there are 8 cells, the total internal resistance is 3 Ω × 8 = 24 Ω.
The formula provides the total internal resistance when connecting cells in parallel.
`therefore 1/"R" = 1/"R"_1 + 1/"R"_2 + 1/"R"_3 + ... + 1/"R"_"L"`
`therefore 1/"R" = 1/24 + ... + 1/24` (6 times)
⇒ R = 4 Ω
Thus, the internal resistance of the battery is 4 Ω. - To calculate the current flowing through the external resistance R, we need to first calculate the total resistance of the circuit.
The external resistance has a resistance of 6 Ω and the internal resistance of the battery is 4 Ω.
When the resistors are connected in series, the total resistance is the sum of the individual resistance.
∴ Rtotal = 6 + 4 = 10 Ω
From ohm's law
I = `"V"/"R" = 16/10 = 1.6` A
Therefore, the current flowing through the external resistor R is 1.6 A.
APPEARS IN
संबंधित प्रश्न
Three resistors 1 Ω, 2 Ω, and 3 Ω are combined in series. What is the total resistance of the combination?
Three identical cells each of emf 2V and internal resistance 10 Ω are connected in series to form a battery. The battery is then connected to a parallel combination of two identical resistors, each of resistance 6 Ω. Find the current delivered by the battery.
Two heating elements of resistances R1 and R2 when operated at a constant supply of voltage, V, consume powers P1 and P2 respectively. Deduce the expressions for the power of their combination whey they are, in turn, connected in (i) series and (ii) parallel across the same voltage supply.
A uniform wire of resistance 50 Ω is cut into 5 equal parts. These parts are now connected in parallel. The equivalent resistance of the combination is ______________ .
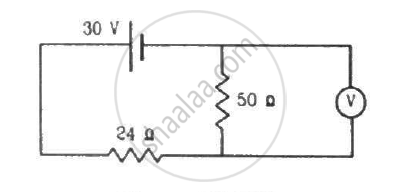
The voltmeter shown in the figure reads 18 V across the 50 Ω resistor. Find the resistance of the voltmeter.
Two resistors R1= 60 Ω and R2 = 90Ω are connected in parallel. If electric power consumed by the resistor R1 is15 W, calculate the power consumed by the resistor R2.
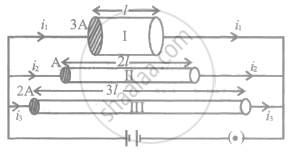
The figure shows three conductors I, II and III of same material, different lengths l, 2l and 3l and of different areas of cross-sections 3A, A and 2A respectively. Arrange them in the increasing order of current drawn from the battery.