Advertisements
Advertisements
प्रश्न
Eight identical cells, each of emf 2V and internal resistance 3 Ω, are connected in series to form a row. Six such rows are connected in parallel to form a battery. This battery is now connected to an external resistor R of resistance 6 Ω. Calculate:
- emf of the battery.
- internal resistance of the battery.
- current flowing through R.
उत्तर
- The emf of each cell is 2 V, and there are 8 cells connected in series. Therefore the emf of the battery is 2 V × 8 = 16 V.
- When cells are connected in series, the total internal resistance is the sum of all the internal resistances of each cell.
Since there are 8 cells, the total internal resistance is 3 Ω × 8 = 24 Ω.
The formula provides the total internal resistance when connecting cells in parallel.
`therefore 1/"R" = 1/"R"_1 + 1/"R"_2 + 1/"R"_3 + ... + 1/"R"_"L"`
`therefore 1/"R" = 1/24 + ... + 1/24` (6 times)
⇒ R = 4 Ω
Thus, the internal resistance of the battery is 4 Ω. - To calculate the current flowing through the external resistance R, we need to first calculate the total resistance of the circuit.
The external resistance has a resistance of 6 Ω and the internal resistance of the battery is 4 Ω.
When the resistors are connected in series, the total resistance is the sum of the individual resistance.
∴ Rtotal = 6 + 4 = 10 Ω
From ohm's law
I = `"V"/"R" = 16/10 = 1.6` A
Therefore, the current flowing through the external resistor R is 1.6 A.
APPEARS IN
संबंधित प्रश्न
Three identical cells each of emf 2V and internal resistance 10 Ω are connected in series to form a battery. The battery is then connected to a parallel combination of two identical resistors, each of resistance 6 Ω. Find the current delivered by the battery.
A uniform wire of resistance 50 Ω is cut into 5 equal parts. These parts are now connected in parallel. The equivalent resistance of the combination is ______________ .
A wire of resistance 15.0 Ω is bent to form a regular hexagon ABCDEFA. Find the equivalent resistance of the loop between the points (a) A and B (b) A and C and (c) Aand D.
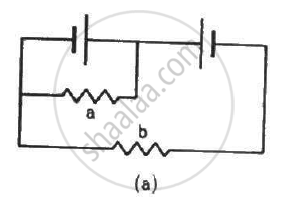
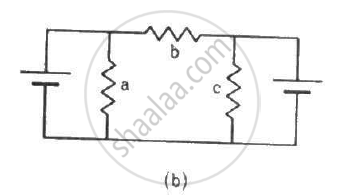
Each of the resistors shown in the figure has a resistance of 10 Ω and each of the batteries has an emf of 10 V. Find the currents flowing through the resistors a and bin the two circuits.
Two voltameters, one with a solution of silver salt and the other with a trivalent-metal salt, are connected in series and a current of 2 A is maintained for 1.50 hours. It is found that 1.00 g of the trivalent metal is deposited. (a) What is the atomic weight of the trivalent metal?
(b) How much silver is deposited during this period? Atomic weight of silver is 107.9 g mol−1.
Two resistors R1= 60 Ω and R2 = 90Ω are connected in parallel. If electric power consumed by the resistor R1 is15 W, calculate the power consumed by the resistor R2.
To get maximum current in a resistance of 3 ohms, one can use n rows of m cells (connected in series) connected in parallel. If the total number of cells is 24 and the internal resistance of a cell is 0.5 ohms then ______.
How many times will the resistance of an identical conductor be increase, if the parallel resistance be change to series one?
An electric cable of copper has just one wire of radius 9 mm. Its resistance is 14Ω. If this single copper wire of the cable is replaced by seven identical well insulated copper wires each of radius 3 mm connected in parallel, then the new resistance of the combination will be:
