Advertisements
Advertisements
Question
If the combination is connected to a battery of emf 20 V and negligible internal resistance, determine the current through each resistor, and the total current drawn from the battery.
Solution
Emf of the battery, V = 20 V
Current (I1) flowing through resistor R1 is given by,
I1 = `"V"/"R"_1`
= `20/2`
= 10 A
Current (I2) flowing through resistor R2 is given by,
I2 = `"V"/"R"_2`
= `20/4`
= 5 A
Current (I3) flowing through resistor R3 is given by,
I3 = `"V"/"R"_3`
= `20/5`
= 4 A
Total current, I = I1 + I2 + I3 = 10 + 5 + 4 = 19 A
Therefore, the current through each resister is 10 A, 5 A, and 4 A respectively and the total current is 19 A.
APPEARS IN
RELATED QUESTIONS
Three resistors 1 Ω, 2 Ω, and 3 Ω are combined in series. What is the total resistance of the combination?
Three resistors 2 Ω, 4 Ω and 5 Ω are combined in parallel. What is the total resistance of the combination?
Three identical cells each of emf 2V and internal resistance 10 Ω are connected in series to form a battery. The battery is then connected to a parallel combination of two identical resistors, each of resistance 6 Ω. Find the current delivered by the battery.
Suppose you have three resistors, each of value 30 Ω. List all the different resistances you can obtain using them.
An ideal battery sends a current of 5 A in a resistor. When another resistor of 10 Ω is connected in parallel, the current through the battery is increased to 6 A. Find the resistance of the first resistor.
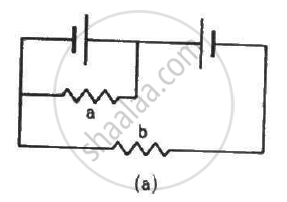
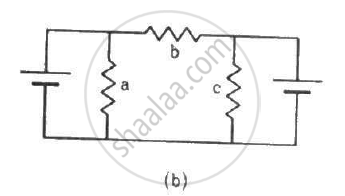
Each of the resistors shown in the figure has a resistance of 10 Ω and each of the batteries has an emf of 10 V. Find the currents flowing through the resistors a and bin the two circuits.
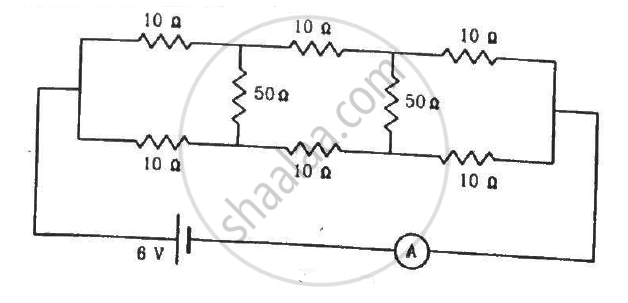
Find the current measured by the ammeter in the circuit shown in the figure.
Two resistors of equal resistances are joined in series and a current is passed through the combination. Neglect any variation in resistance as the temperature changes. In a given time interval,
(a) equal amounts of thermal energy must be produced in the resistors
(b) unequal amounts of thermal energy may be produced
(c) the temperature must rise equally in the resistors
(d) the temperature may rise equally in the resistors
An ammeter together with an unknown resistance in series is connected across two identical batteries each of emf 1.5 V. When the batteries are connected in series, the galvanometer records a current of 1A and when the batteries are in parallel, the current is 0.6A. Then the internal resistance of the battery is ______.
In parallel combination of n cells, we obtain ______.
An electric current is passed through a circuit containing two wires of the same material, connected in parallel. If the lengths and radii of the wires are in the ratio of 3:2 and 2:3, then the ratio of the current passing through the wire will be ____________.
The instantaneous values of emf and the current in a series ac circuit are-
E = Eo Sin ωt and I = Io sin (ωt+π/3) respectively, then it is ______.
If two resistors of resistances R1 = (4 ± 0.5) Ω and R2 = (16 ± 0.5) Ω are connected in series. The eqivalent resistance with the limits of percentage error is ______.
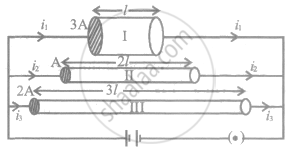
The figure shows three conductors I, II and III of same material, different lengths l, 2l and 3l and of different areas of cross-sections 3A, A and 2A respectively. Arrange them in the increasing order of current drawn from the battery.
The effective resistance of a parallel connection that consists of four wires of equal length, equal area of cross-section and same material is 0.25 Ω. What will be the effective resistance if they are connected in series?
Let there be n resistors R1............Rn with Rmax = max (R1......... Rn) and Rmin = min {R1..... Rn}. Show that when they are connected in parallel, the resultant resistance RP < R min and when they are connected in series, the resultant resistance RS > Rmax. Interpret the result physically.
