Advertisements
Advertisements
प्रश्न
Show that the points A(- 2, 5), B(2, – 3) and C(0, 1) are collinear.
उत्तर
m1 = Slope ofAB
= `(-3 - 5)/(2 - (-2)) = (8)/(4)` = -2
m2 = slop of BC
= `(1 - (-3))/(0 - 2) = (4)/(-2)` = -2
Hence m1 = m2 = -2
So, AB is parallel to BC.
But B is common to AB and BC.
Hence, A, B and C must lies on the same line.
Hence proved.
APPEARS IN
संबंधित प्रश्न
Find the slope of the line passing through the points A(-2, 1) and B(0, 3).
Without using the distance formula, show that the points A(4, 5), B(1, 2), C(4, 3) and D(7, 6) are the vertices of a parallelogram.
Find x, if the slope of the line joining (x, 2) and (8, −11) is `−3/4`.
Find the slope and the inclination of the line AB if : A = (−3, −2) and B = (1, 2)
Plot the points A(1, 1), B(4, 7) and C(4, 10) on a graph paper. Connect A and B and also A and C.
Which segment appears to have the steeper slope, AB or AC?
Justify your conclusion by calculating the slopes of AB and AC.
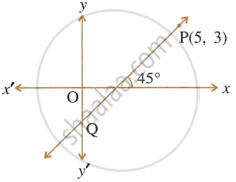
The line through P(5, 3) intersects y-axis at Q.
- Write the slope of the line.
- Write the equation of the line.
- Find the co-ordinates of Q.
Determine whether the following point is collinear.
D(–2, –3), E(1, 0), F(2, 1)
Fill in the blank using correct alternative.
A line makes an angle of 30° with the positive direction of X– axis. So the slope of the line is ______.
Find the slope of a line parallel to the given line 5x-y = 10
Find the slope of the line passing through the points A(4,7) and B(2,3).
