Advertisements
Advertisements
प्रश्न
सोबतच्या आकृतीत, केंद्र C असलेेले वर्तुळ केंद्र D असलेल्या वर्तुळाला बिंदू E मध्ये आतून स्पर्श करते. बिंदू D हा आतील वर्तुळावर आहे. बाहेरील वर्तुळाची जीवा EB ही आतील वर्तुळाला बिंदू A मध्ये छेदते. तर सिद्ध करा, की रेख EA ≅ रेख AB.
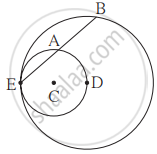
उत्तर
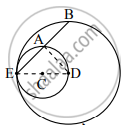
पक्ष: केंद्र C असलेले वर्तुळ केंद्र D असलेल्या वर्तुळाला आतून स्पर्श करते.
साध्य: रेख EA ≅ रेख AB
रचना: रेख ED व रेख DA काढा.
सिद्धता:
E - C - D ........[स्पर्शवर्तुळांचे प्रमेय]
रेख ED ही लहान वर्तुळाचा व्यास आहे.
∴ ∠EAD = 90° ......[अर्धवर्तुळात अंतर्लिखित कोन]
∴ रेख AD ⊥ जीवा EB
∴ रेख EA ≅ रेख AB .....[वर्तुळकेंद्रापासून जीवेवर टाकलेला लंब जीवेस दुभागतो.]
APPEARS IN
संबंधित प्रश्न
दोन अंतर्स्पर्शी वर्तुळांच्या त्रिज्या अनुक्रमे 3.5 सेमी व 4.8 सेमी आहेत, तर त्यांच्या केंद्रांतील अंतर किती आहे?
बाह्यस्पर्शी असलेल्या दोन वर्तुळांच्या त्रिज्या अनुक्रमे 5.5 सेमी व 4.2 सेमी असतील तर त्यांच्या केंद्रांतील अंतर किती असेल?
प्रत्येकी 3 सेमी त्रिज्येची, केंद्र A, B व C असणारी तीन वर्तुळे अशी काढा, की प्रत्येक वर्तुळ इतर दोन वर्तुळांना स्पर्श करेल.
सोबतच्या आकृतीत, केंद्र X आणि Y असलेली वर्तुळे परस्परांना बिंदू Z मध्ये स्पर्श करतात. बिंदू Z मधून जाणारी वृत्तछेदिका त्या वर्तुळांना अनुक्रमे बिंदू A व बिंदू B मध्ये छेदते. तर सिद्ध करा,
त्रिज्या XA || त्रिज्या YB
खाली दिलेल्या सिद्धतेतील रिकाम्या जागा भरून पूर्ण सिद्धता लिहून काढा.
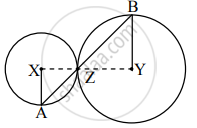
रचना : रेख XZ आणि YZ काढा.
सिद्धता : स्पर्शवर्तुळांच्या प्रमेयानुसार, बिंदू X, Z, Y हे `square`
∴ ∠XZA ≅ `square` ............[विरुद्ध कोन]
∠XZA = ∠BZY = p मानू ............ (i)
आता, रेख XA ≅ रेख XZ ...........[एकाच वर्तुळाच्या त्रिज्या]
∴ ∠XAZ = `square` = p ............ (ii) (समद्विभुज त्रिकोणाचे प्रमेय)
तसेच रेख YB ≅ YZ ..................[एकाच वर्तुळाच्या त्रिज्या]
∴ ∠BZY = `square` = p (iii) [समद्विभुज त्रिकोणाचे प्रमेय]
∴ (i), (ii) व (iii) वरून,
∠XAZ = `square`
∴ त्रिज्या XA || त्रिज्या YB ................[`square`]
