Advertisements
Advertisements
प्रश्न
Solve the following problem :
Following table shows the amount of sugar production (in lac tonnes) for the years 1971 to 1982.
| Year | 1971 | 1972 | 1973 | 1974 | 1975 | 1976 | 1977 | 1978 | 1979 | 1980 | 1981 | 1982 |
| Production | 1 | 0 | 1 | 2 | 3 | 2 | 3 | 6 | 5 | 1 | 4 | 10 |
Fit a trend line to the above data by graphical method.
उत्तर
Taking year on X-axis and production on Y-axis, we plot the points for production corresponding to years. Joining these points we get the graph of time series. We fit a trend line as shown in the graph.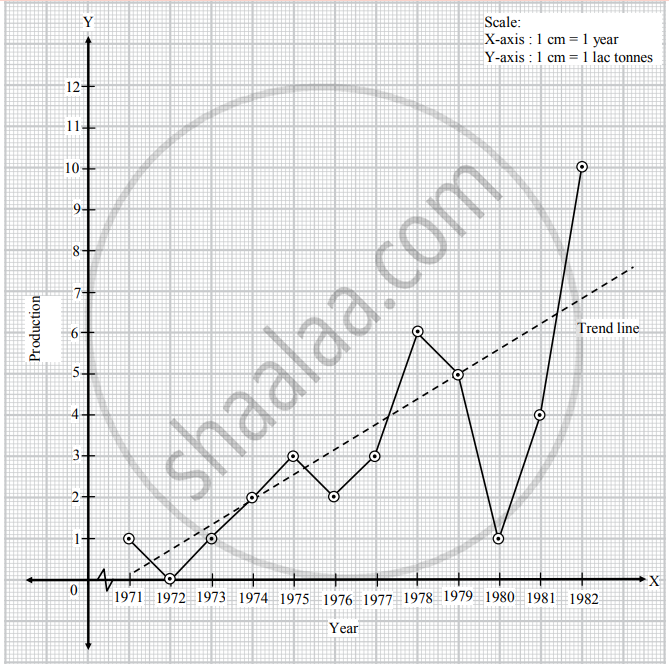
APPEARS IN
संबंधित प्रश्न
Obtain the trend values for the data in using 4-yearly centered moving averages.
| Year | 1976 | 1977 | 1978 | 1979 | 1980 | 1981 | 1982 | 1983 | 1984 | 1985 |
| Index | 0 | 2 | 3 | 3 | 2 | 4 | 5 | 6 | 7 | 10 |
Fit a trend line to the data in Problem 7 by the method of least squares. Also, obtain the trend value for the year 1990.
The simplest method of measuring trend of time series is ______.
Fill in the blank :
The method of measuring trend of time series using only averages is _______
State whether the following is True or False :
Graphical method of finding trend is very complicated and involves several calculations.
Solve the following problem :
The following table shows the production of pig-iron and ferro- alloys (‘000 metric tonnes)
| Year | 1974 | 1975 | 1976 | 1977 | 1978 | 1979 | 1980 | 1981 | 1982 |
| Production | 0 | 4 | 9 | 9 | 8 | 5 | 4 | 8 | 10 |
Fit a trend line to the above data by graphical method.
Solve the following problem :
Obtain trend values for the data in Problem 7 using 4-yearly moving averages.
Solve the following problem :
Obtain trend values for data in Problem 13 using 4-yearly moving averages.
Obtain trend values for data in Problem 19 using 3-yearly moving averages.
Choose the correct alternative:
Moving averages are useful in identifying ______.
State whether the following statement is True or False:
Least squares method of finding trend is very simple and does not involve any calculations
Following table shows the amount of sugar production (in lac tons) for the years 1971 to 1982
| Year | 1971 | 1972 | 1973 | 1974 | 1975 | 1976 |
| Production | 1 | 0 | 1 | 2 | 3 | 2 |
| Year | 1977 | 1978 | 1979 | 1980 | 1981 | 1982 |
| Production | 4 | 6 | 5 | 1 | 4 | 10 |
Fit a trend line by the method of least squares
Obtain the trend values for the data, using 3-yearly moving averages
| Year | 1976 | 1977 | 1978 | 1979 | 1980 | 1981 |
| Production | 0 | 4 | 4 | 2 | 6 | 8 |
| Year | 1982 | 1983 | 1984 | 1985 | 1986 | |
| Production | 5 | 9 | 4 | 10 | 10 |
The following table shows the production of gasoline in U.S.A. for the years 1962 to 1976.
| Year | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 | 1968 | 1969 |
| Production (million barrels) |
0 | 0 | 1 | 1 | 2 | 3 | 4 | 5 |
| Year | 1970 | 1971 | 1972 | 1973 | 1974 | 1975 | 1976 | |
| Production (million barrels) |
6 | 7 | 8 | 9 | 8 | 9 | 10 |
- Obtain trend values for the above data using 5-yearly moving averages.
- Plot the original time series and trend values obtained above on the same graph.
Obtain trend values for data, using 3-yearly moving averages
Solution:
| Year | IMR | 3 yearly moving total |
3-yearly moving average (trend value) |
| 1980 | 10 | – | – |
| 1985 | 7 | `square` | 7.33 |
| 1990 | 5 | 16 | `square` |
| 1995 | 4 | 12 | 4 |
| 2000 | 3 | 8 | `square` |
| 2005 | 1 | `square` | 1.33 |
| 2010 | 0 | – | – |
Fit equation of trend line for the data given below.
| Year | Production (y) | x | x2 | xy |
| 2006 | 19 | – 9 | 81 | – 171 |
| 2007 | 20 | – 7 | 49 | – 140 |
| 2008 | 14 | – 5 | 25 | – 70 |
| 2009 | 16 | – 3 | 9 | – 48 |
| 2010 | 17 | – 1 | 1 | – 17 |
| 2011 | 16 | 1 | 1 | 16 |
| 2012 | 18 | 3 | 9 | 54 |
| 2013 | 17 | 5 | 25 | 85 |
| 2014 | 21 | 7 | 49 | 147 |
| 2015 | 19 | 9 | 81 | 171 |
| Total | 177 | 0 | 330 | 27 |
Let the equation of trend line be y = a + bx .....(i)
Here n = `square` (even), two middle years are `square` and 2011, and h = `square`
The normal equations are Σy = na + bΣx
As Σx = 0, a = `square`
Also, Σxy = aΣx + bΣx2
As Σx = 0, b = `square`
Substitute values of a and b in equation (i) the equation of trend line is `square`
To find trend value for the year 2016, put x = `square` in the above equation.
y = `square`
Obtain the trend values for the following data using 5 yearly moving averages:
| Year | 2000 | 2001 | 2002 | 2003 | 2004 |
| Production xi |
10 | 15 | 20 | 25 | 30 |
| Year | 2005 | 2006 | 2007 | 2008 | 2009 |
| Production xi |
35 | 40 | 45 | 50 | 55 |
Complete the following activity to fit a trend line to the following data by the method of least squares.
| Year | 1975 | 1976 | 1977 | 1978 | 1979 | 1980 | 1981 | 1982 | 1983 |
| Number of deaths | 0 | 6 | 3 | 8 | 2 | 9 | 4 | 5 | 10 |
Solution:
Here n = 9. We transform year t to u by taking u = t - 1979. We construct the following table for calculation :
| Year t | Number of deaths xt | u = t - 1979 | u2 | uxt |
| 1975 | 0 | - 4 | 16 | 0 |
| 1976 | 6 | - 3 | 9 | - 18 |
| 1977 | 3 | - 2 | 4 | - 6 |
| 1978 | 8 | - 1 | 1 | - 8 |
| 1979 | 2 | 0 | 0 | 0 |
| 1980 | 9 | 1 | 1 | 9 |
| 1981 | 4 | 2 | 4 | 8 |
| 1982 | 5 | 3 | 9 | 15 |
| 1983 | 10 | 4 | 16 | 40 |
| `sumx_t` =47 | `sumu`=0 | `sumu^2=60` | `square` |
The equation of trend line is xt= a' + b'u.
The normal equations are,
`sumx_t = na^' + b^' sumu` ...(1)
`sumux_t = a^'sumu + b^'sumu^2` ...(2)
Here, n = 9, `sumx_t = 47, sumu= 0, sumu^2 = 60`
By putting these values in normal equations, we get
47 = 9a' + b' (0) ...(3)
40 = a'(0) + b'(60) ...(4)
From equation (3), we get a' = `square`
From equation (4), we get b' = `square`
∴ the equation of trend line is xt = `square`
