Advertisements
Advertisements
प्रश्न
Solve the following problem :
If a fair coin is tossed 4 times, find the probability that it shows head in the first 2 tosses and tail in last 2 tosses.
उत्तर
Let X denote the number of heads.
P(getting head) = p = `(1)/(2)`
∴ q = 1 – p = `1 - (1)/(2) = (1)/(2)`
Given, n = 4
∴ X ∼ B`(4, 1/2)`
The p.m.f of X is given by
P(X = x) = `""^4"C"_x (1/2)^x (1/2)^(4 - x), x` = 0, 1,....,4
P(getting head in the first 2 tosses and tail in last 2 tosses.)
= P[X = 2] = `4C_2(1/2)^4`
=`(4xx3)/(2xx1)xx1/16`
= `6 xx 1/16`
= `3/8`
APPEARS IN
संबंधित प्रश्न
Let X be a random variable which assumes values x1, x2, x3, x4 such that 2P (X = x1) = 3P(X = x2) = P (X = x3) = 5 P (X = x4). Find the probability distribution of X.
Two dice are thrown together and the number appearing on them noted. X denotes the sum of the two numbers. Assuming that all the 36 outcomes are equally likely, what is the probability distribution of X?
Two cards are drawn successively with replacement from well shuffled pack of 52 cards. Find the probability distribution of the number of aces.
From a lot containing 25 items, 5 of which are defective, 4 are chosen at random. Let X be the number of defectives found. Obtain the probability distribution of X if the items are chosen without replacement .
Let X represent the difference between the number of heads and the number of tails when a coin is tossed 6 times. What are the possible values of X?
Let, X denote the number of colleges where you will apply after your results and P(X = x) denotes your probability of getting admission in x number of colleges. It is given that
where k is a positive constant. Find the value of k. Also find the probability that you will get admission in (i) exactly one college (ii) at most 2 colleges (iii) at least 2 colleges.
Find the mean and standard deviation of each of the following probability distribution :
| xi : | -5 | -4 | 1 | 2 |
| pi : | \[\frac{1}{4}\] | \[\frac{1}{8}\] | \[\frac{1}{2}\] | \[\frac{1}{8}\] |
Find the mean and standard deviation of each of the following probability distribution :
| xi : | 1 | 2 | 3 | 4 |
| pi : | 0.4 | 0.3 | 0.2 | 0.1 |
Find the mean and standard deviation of each of the following probability distribution :
| xi: | 0 | 1 | 3 | 5 |
| pi : | 0.2 | 0.5 | 0.2 | 0.1 |
Find the mean variance and standard deviation of the following probability distribution
| xi : | a | b |
| pi : | p | q |
A fair coin is tossed four times. Let X denote the number of heads occurring. Find the probability distribution, mean and variance of X.
A die is tossed twice. A 'success' is getting an odd number on a toss. Find the variance of the number of successes.
If the probability distribution of a random variable X is as given below:
Write the value of P (X ≤ 2).
| X = xi : | 1 | 2 | 3 | 4 |
| P (X = xi) : | c | 2c | 4c | 4c |
If a random variable X has the following probability distribution:
| X : | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| P (X) : | a | 3a | 5a | 7a | 9a | 11a | 13a | 15a | 17a |
then the value of a is
A random variable X takes the values 0, 1, 2, 3 and its mean is 1.3. If P (X = 3) = 2 P (X = 1) and P (X = 2) = 0.3, then P (X = 0) is
Find the probability distribution of the number of doublets in three throws of a pair of dice and find its mean.
Two fair coins are tossed simultaneously. If X denotes the number of heads, find the probability distribution of X. Also find E(X).
The following data gives the marks of 20 students in mathematics (X) and statistics (Y) each out of 10, expressed as (x, y). construct ungrouped frequency distribution considering single number as a class :
(2, 7) (3, 8) (4, 9) (2, 8) (2, 8) (5, 6) (5 , 7) (4, 9) (3, 8) (4, 8) (2, 9) (3, 8) (4, 8) (5, 6) (4, 7) (4, 7) (4, 6 ) (5, 6) (5, 7 ) (4, 6 )
If random variable X has probability distribution function.
f(x) = `c/x`, 1 < x < 3, c > 0, find c, E(x) and Var(X)
If X ∼ N (4,25), then find P(x ≤ 4)
Solve the following :
Identify the random variable as either discrete or continuous in each of the following. Write down the range of it.
20 white rats are available for an experiment. Twelve rats are male. Scientist randomly selects 5 rats number of female rats selected on a specific day
The probability that a bulb produced by a factory will fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5) that fuse after 200 days of use. Find the probability of X = 0
The probability that a bulb produced by a factory will fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5) that fuse after 200 days of use. Find the probability of (i) X = 0, (ii) X ≤ 1, (iii) X > 1, (iv) X ≥ 1.
Defects on plywood sheet occur at random with the average of one defect per 50 Sq.ft. Find the probability that such a sheet has no defect
Solve the following problem :
Following is the probability distribution of a r.v.X.
| x | – 3 | – 2 | –1 | 0 | 1 | 2 | 3 |
| P(X = x) | 0.05 | 0.1 | 0.15 | 0.20 | 0.25 | 0.15 | 0.1 |
Find the probability that X is even.
Solve the following problem :
The probability that a bomb will hit the target is 0.8. Find the probability that, out of 5 bombs, exactly 2 will miss the target.
Solve the following problem :
The probability that a component will survive a check test is 0.6. Find the probability that exactly 2 of the next 4 components tested survive.
Let the p.m.f. of a random variable X be P(x) = `(3 - x)/10`, for x = −1, 0, 1, 2 = 0, otherwise Then E(x) is ______
For the random variable X, if V(X) = 4, E(X) = 3, then E(x2) is ______
A discrete random variable X has the probability distribution given as below:
| X | 0.5 | 1 | 1.5 | 2 |
| P(X) | k | k2 | 2k2 | k |
Find the value of k
Consider the probability distribution of a random variable X:
| X | 0 | 1 | 2 | 3 | 4 |
| P(X) | 0.1 | 0.25 | 0.3 | 0.2 | 0.15 |
Calculate `"V"("X"/2)`
The probability distribution of a random variable X is given below:
| X | 0 | 1 | 2 | 3 |
| P(X) | k | `"k"/2` | `"k"/4` | `"k"/8` |
Find P(X ≤ 2) + P (X > 2)
The probability distribution of a random variable x is given as under:
P(X = x) = `{{:("k"x^2, "for" x = 1"," 2"," 3),(2"k"x, "for" x = 4"," 5"," 6),(0, "otherwise"):}`
where k is a constant. Calculate E(X)
The probability distribution of a discrete random variable X is given below:
| X | 2 | 3 | 4 | 5 |
| P(X) | `5/"k"` | `7/"k"` | `9/"k"` | `11/"k"` |
The value of k is ______.
Two numbers are selected from first six even natural numbers at random without replacement. If X denotes the greater of two numbers selected, find the probability distribution of X.
Kiran plays a game of throwing a fair die 3 times but to quit as and when she gets a six. Kiran gets +1 point for a six and –1 for any other number.
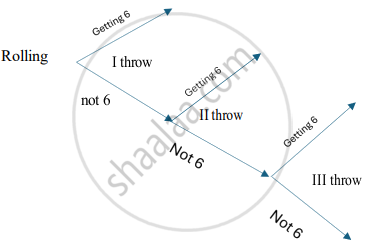
- If X denotes the random variable “points earned” then what are the possible values X can take?
- Find the probability distribution of this random variable X.
- Find the expected value of the points she gets.
