Advertisements
Advertisements
प्रश्न
State and prove Euler’s Theorem for three variables.
उत्तर
Statement: If u=f(x, y, z) is a homogeneous function of degree n, then -`x(delu)/(delx)+y(delu)/(dely)+z(delu)/(delz)=n u`
Let, u=f(x, y, z) is a homogeneous function of degree n.
Putting X = x t, Y = y t, Z = z t.
f(X,Y,Z) = tn f(x,y,z) ………. (1)
Diff LHS w.r.t t,
`(delf)/(delt)=(delf)/(delx).(delx)/(delt)+(delfdely)/(delydelt)+(delfdelz)/(delzdelt)`
`(delf)/(delt)=x(delf)/(delx).+y(delf)/(dely)+z(delf)/(delz)`…… (2)
Diff RHS w.r.t. t,
`(delf)/(delt)=nt^(n-1)f(x,y,z)`
Now put t = 1, we get `(delf)/(delt)=nf(x,y,z)`……… (3)
From equation 2 and 3, we get
`x(delf)/(delx).+y(delf)/(dely)+z(delf)/(delz)=nf(x,y,z)`
`x(delf)/(delx).+y(delf)/(dely)+z(delf)/(delz)=n u`
Hence proved
APPEARS IN
संबंधित प्रश्न
If x = u+v+w, y = uv+vw+uw, z = uvw and φ is a function of x, y and z
Prove that 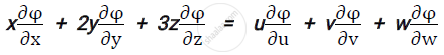
If tan(θ+iφ)=tanα+isecα
Prove that
1)`e^(2varphi)=cot(varphi/2)`
2) `2theta=npi+pi/2+alpha`
State Euler’s theorem on homogeneous function of two variables and if `u=(x+y)/(x^2+y^2)` then evaluate `x(delu)/(delx)+y(delu)/(dely`
If u =`f((y-x)/(xy),(z-x)/(xz)),` show that `x^2(delu)/(delx)+y^2(delu)/(dely)+z^2(delu)/(delz)=0`.
If `u=sin^(-1)((x+y)/(sqrtx+sqrty))`,Prove that
`x^2u_(x x)+2xyu_(xy)+y^2u_(yy)=(-sinu.cos2u)/(4cos^3u)`
State and Prove Euler’s Theorem for three variables.
If z = f (x, y) where x = eu +e-v, y = e-u - ev then prove that `(delz)/(delu)-(delz)/(delv)=x(delz)/(delx)-y(delz)/(dely).`
If U `=sin^(-1)[(x^(1/3)+y^(1/3))/(x^(1/2)+y^(1/2))]`prove that `x^2(del^2u)/(del^2x)+2xy(del^2u)/(delxdely)+y^2(del^2u)/(del^2y)=(tanu)/144[tan^2"U"+13].`
