Advertisements
Advertisements
प्रश्न
Answer the following question.
State the formula for calculating work done by a force. Are there any conditions or limitations in using it directly? If so, state those clearly. Is there any mathematical way out for it? Explain.
उत्तर
- Suppose a constant force `vec"F"` acting on a body produces a displacement `vec"s"` in the body along the positive X-direction. Then the work done by the force is given as,
W = F·s cos θ
Where θ is the angle between the applied force and displacement. - If displacement is in the direction of the force applied, θ = 00
W = `vec"F"*vec"s"`
Conditions/limitations for application of work formula:
- The formula for work done is applicable only if both force `vec"F"` and displacement `vec"s"` are constant and finite i.e., it cannot be applied when the force is variable.
- The formula is not applicable in several real-life situations like lifting an object through several thousand kilometers since the gravitational force is not constant. It is not applicable to viscous forces like fluid resistance as they depend upon speed and thus are often not constant with time.
- The method of integration has to be applied to find the work done by a variable force.
Integral method to find work done by a variable force:

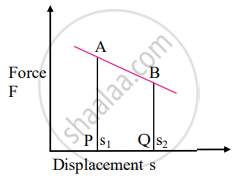
- Let the force vary non-linearly in magnitude between points A and B as shown in the above figure.
- In order to calculate the total work done during the displacement from s1 to s2, we need to use integration. For integration, we need to divide the displacement into large numbers of infinitesimal (infinitely small) displacements.
- Let at P1, the magnitude of force be F = P1P1'. Due to this force, the body displaces through infinitesimally small-displacement ds, in the direction of the force. It moves from P1 to P2.
∴ `"d"vec"s" = vec("P"_1"P"_2)` - But direction of force and displacement are same, we have
`"d"vec"s" = P_1^'P_2^'` - `"d"vec"s"` is so small that the force F is practically constant for the displacement. As the force is constant, the area of the strip `vec"F"`. `"d"vec"s"` is the work done dW for this displacement.
- Hence, small work done between P1 to P2 is dW and is given by
dW = `vec"F" * "d"vec"s" = "P"_1"P"_1^' xx "P"_1^'"P"_2^'`
= Ares of the strip P1P2P2'P1'. - The total work done can be found out by dividing the portion AB into small strips like P1P2P2'P1' and taking sum of all the areas of the strips.
∴ W = \[\int_{s_1}^{s_2}\vec{F}.d\vec{s}\] = Area ABB'A' - Method of integration is applicable if the exact way of variation in `vec"F" and vec"s"` is known and that function is integrable.
- The work done by the non-linear variable force is represented by the area under the portion of the force-displacement graph.
- Similarly, in the case of a linear variable force, the area under the curve from s1 to s2 (trapezium APQB) gives total work done W in the following figure.
APPEARS IN
संबंधित प्रश्न
Answer the following question.
In the following table, every entry on the left column can match with any number of entries on the right side. Pick up all those and write respectively against A, B, C and D.
| Name of the force | Type of the force | ||
| A | Force due to tension in a string | P | EM force |
| B | Normal force | Q | Reaction force |
| C | Frictional force | R | Conservative force |
| D | Resistive force offered by air or water for objects moving through it. | S | Non-conservative force |
Among the four fundamental forces, only one force governs your daily life almost entirely. Justify the statement by stating that force.
Find the odd man out:
Answer the following question.
You are sitting next to your friend on ground. Is there any gravitational force of attraction between you two? If so, why are you not coming together naturally? Is any force other than the gravitational force of the earth coming in the picture?
Answer the following question.
Distinguish between real and pseudo force.
Answer the following question.
Distinguish between conservative and nonconservative forces.
Answer the following question.
Distinguish between contact and non-contact forces
40000 litre of oil of density 0.9 g/cc is pumped from an oil tanker ship into a storage tank at 10 m higher level than the ship in half an hour. What should be the power of the pump?
Solve the following problem.
Power is the rate of doing work or the rate at which energy is supplied to the system. A constant force F is applied to a body of mass m. Power delivered by the force at time t from the start is proportional to ______.
Derive the expression for power in terms of F, m, and t.
Solve the following problem.
In the following table, every item on the left side can match with any number of items on the right-hand side. Select all those.
| Types of collision | Illustrations | ||
| a. | Elastic collision | i. | A ball hit by a bat. |
| b. | Inelastic collision | ii. | Molecular collisions responsible for pressure exerted by a gas. |
| c. | Perfectly inelastic collision | iii. | A stationary marble A is hit by marble B and the marble B comes to rest. |
| d. | Head-on collision | iv. | A blob of clay dropped on the ground sticks to the ground. |
| v. | Out of anger, giving a kick to a wall. | ||
| vi. | A striker hits the boundary of a carrom board in a direction perpendicular to the boundary and rebounds. | ||
Two spheres of masses m and M are situated in air and the gravitational force between them is F. The space around the masses is now filled with a liquid of specific gravity 3. The gravitational force will now be ______
Two bodies A and B of equal mass are suspended from two separate massles springs of force constant k1 and k2, respectively. The bodies oscillate vertically such that their maximum velocities are equal. The ratio of the amplitudes of body A to that of body B is ______.
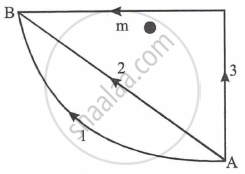
If W1, W2 and W3 represent the work done in moving a particle from A to B along three different paths 1, 2 and 3 (as shown in fig) in the gravitational field of the point mass 'm'. Find the correct relation between W1, W2 and W3.
In air, a charged soap bubble of radius 'R' breaks into 27 small soap bubbles of equal radius 'r '. Then the ratio of mechanical force acting per unit area of big soap bubble to that of a small soap bubble is ______.
A body of mass 'm' begins to move under the action of time-dependent force `vec"F" = ("t"hat"i" + 2"t"^2hat"j")`N where `hat"i" and hat"j"` are unit vectors along x and y axis respectively. The power developed by the force in watt at time 't' is ______.
What is the amount of work done by a person when
- he holds a mass of 2 kg for 5 second and
- he lifts the same mass through 1 meter to keep it on the top of a table? g = 9.8 m/s2
A force of F = `("x"/2 + 15) "N"` acts on a particle. If x 2 is in metre, calculate the work done by the force during the displacement of the particle from x = 0 to x = 4 m
Work done in sliding a 1 kg block up a rough inclined plane of height 5 m is 100 J. Work done against the friction is ______.
(g = 10 m/s2)
'n' number of balls each having mass 'm' and velocity 'u' hit a wall elastically and normally in 2 seconds. The force exerted by them on the wall is ______.
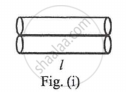
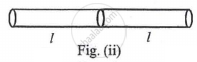
Two rods of same length and transfer a given amount of heat 12 second, when they are joined as shown in figure (i), But when they are joined as shown in figure (ii), then they will transfer same heat in same conditions in ______.
A gardener pushes a lawn roller through a distance of 20 m. If he applies a force of 30 kg-wt in a direction inclined at 60° to the ground, the work done by the gardener in pushing the roller is ______.
`["g" = 9.8 "m""/""s"^2, sin30^circ = cos60^circ = 1/2, cos30^circ = sin60^circ = sqrt3/2]`
A uniform beam is balanced at its mid-point an object placed on the beam as shown.
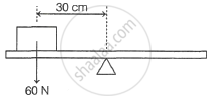
Which force will rebalance the beam?
