Advertisements
Advertisements
प्रश्न
Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular.
उत्तर
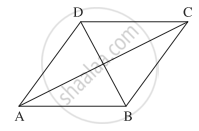
Let ABCD be a quadrilateral in which
`|bar"AB"| = |bar"BC"| = |bar"CD"| = |bar"DA"|` ....(1)
and AB || DC and AD || BC
∴ `bar"AB" = bar"DC"` and `bar"AD" = bar"BC"` ...(2)
Now, `bar"AC" = bar"AB" + bar"BC"`
and `bar"BD" = bar"BA" + bar"AD" = - bar"AB" + bar"BC"` ...[By(2)]
`= bar"BC" - bar"AB"`
∴ `bar"AC".bar"BD" = (bar"AB" + bar"BC").(bar"BC" - bar"AB")`
`= bar"AB".(bar"BC" - bar"AB") + bar"BC" . (bar"BC" - bar"AB")`
`= bar"AB".bar"BC" - bar"AB".bar"AB" + bar"BC".bar"BC" - bar"BC".bar"AB"`
`= |bar"BC"|^2 - |bar"AB"|^2` ....`[∵ bar"AB".bar"BC" = bar"BC".bar"AB"]`
= 0 ...[By(1)]
∵ `bar"AC", bar"BD"` are non-zero vectors
∴ `bar"AC"` is perpendicular to `bar"BD"`
Hence, the diagonals are perpendicular.
APPEARS IN
संबंधित प्रश्न
If `veca` and `vecb` are two vectors perpendicular to each other, prove that `(veca + vecb)^2 = (veca - vecb)^2`
If `hat"p", hat"q"` and `hat"r"` are unit vectors `hat"p"+hat "r" = hat "q"`, find `hat"p".hat"q".`
If `bar"p", bar"q"` and `bar"r"` are unit vectors, find `bar"p".bar"r".`
The direction ratios of `bar"AB"` are −2, 2, 1. If A = (4, 1, 5) and l(AB) = 6 units, find B.
If `bar"a" = 2hat"i" + 3hat"j" - hat"k"`, `bar"b" = hat"i" - 4hat"j" + 2hat"k"`, find `(bar"a" + bar"b") xx (bar"a" - bar"b")`
Find a unit vector perpendicular to the vectors `hat"j" + 2hat"k"` and `hat"i" + hat"j"`.
Find `bar"u".bar"v"` if `|bar"u"| = 2, |bar"v"| = 5, |bar"u" xx bar"v"| = 8`
Prove that `2(bar"a" - bar"b") xx 2(bar"a" + bar"b") = 8(bar"a" xx bar"b")`
If `bar"a" = hat"i" - 2hat"j" + 3hat"k"` , `bar"b" = 4hat"i" - 3hat"j" + hat"k"` , `bar"c" = hat"i" - hat"j" + 2hat"k"` verify that `bar"a"xx(bar"b" + bar"c") = bar"a" xx bar"b" + bar"a" xx bar"c"`
Find the area of the parallelogram whose adjacent sides are `bar"a" = 2hat"i" - 2hat"j" + hat"k"` and `bar"b" = hat"i" - 3hat"j" - 3hat"k"`
Show that vector area of a parallelogram ABCD is `1/2 (bar"AC" xx bar"BD")` where AC and BD are its diagonals.
Find the area of parallelogram whose diagonals are determined by the vectors `bar"a" = 3hat"i" - hat"j" - 2hat"k"` and `bar"b" = - hat"i" + 3hat"j" - 3hat"k"`.
Find `bar"a"` if `bar"a" xx hat"i" + 2bar"a" - 5hat"j" = bar"0"`
Find the direction ratios of a vector perpendicular to the two lines whose direction ratios are - 2, 1, - 1 and - 3, - 4, 1
Prove that the two vectors whose direction cosines are given by relations al + bm + cn = 0 and fmn + gnl + hlm = 0 are perpendicular, if `"f"/"a" + "g"/"b" + "h"/"c" = 0`
If A(1, 2, 3) and B(4, 5, 6) are two points, then find the foot of the perpendicular from the point B to the line joining the origin and the point A.
The value of `hat"i"*(hat"j" xx hat"k") + hat"j"*(hat"i" xx hat"k") + hat"k"*(hat"i" xx hat"j")`.
The area of triangle ABC in which c = 8 , b = 3, ∠A = 60° is ______
If `overlinea = hati + hatj + hatk` and `overlinec = hatj - hatk` and `overlineb` is a vector satisfying `overlinea xx overlineb = overlinec` and `overlinea . overlineb = 3`, then `3|overlineb|^2` is equal to ______
If the vectors `ahat("i")+hat("j")+hat("k"), hat("i")+bhat("j")+hat("k")` and `hat("i")+hat("j")+chat("k")` are coplanar (a ≠ b ≠ c ≠ 1), then the value of abc - (a + b + c) = ______.
If `bar"a"` makes an acute angle with `bar"b", bar"r"*bar"a"` = 0 and `bar"r"xx bar"b" = bar"c" xx bar"b"`, then `bar"r"` = ______.
If `veca, vecb, vecc` are vectors such that `[(veca, vecb, vecc)]` = 4, then `[(veca xx vecb, vecb xx vecc, vecc xx veca)]` = ______.
Find two unit vectors each of which is perpendicular to both `baru "and" barv`, where `baru =2hati + hatj - 2hatk, barv =hati + 2hatj - 2hatk `
Find two unit vectors each of which is perpendicular to both `\overline "u" and \overline "v",` where ` \overline "u" = 2hati + hatj - 2hatk, \overline "v" = hati + 2hatj - 2hatk`
If a vector has direction angles 45º and 60º find the third direction angle.
If a vector has direction angles 45° and 60° find the third direction angle.
Find the direction ratios of a line perpendicular to both the lines whose direction ratios are 3, –2, 1 and 2, 4, –2
Find two unit vectors each of which is perpendicular to both `baruandbarv, "where" baru=2hati+hatj-2hatk, barv=hati+2hatj-2hatk`.
Find two unit vectors each of which is perpendicular to both `baru and barv`, where `baru = 2hati + hatj - 2hatk, barv = hati + 2hatj - 2hatk`
Find two unit vectors each of which is perpendicular to both `baru and barv, "where" baru = 2hati + hatj - 2hatk, barv = hati + 2hatj - 2hatk`
If a vector has direction angles 45ºand 60º find the third direction angle.
Find two unit vectors each of which is perpendicular to both `baru and barv , "where" baru = 2hati + hatj - 2hatk, barv = hati + 2hatj -2hatk`
