Advertisements
Advertisements
प्रश्न
If A(1, 2, 3) and B(4, 5, 6) are two points, then find the foot of the perpendicular from the point B to the line joining the origin and the point A.
उत्तर
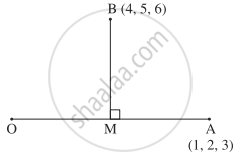
Let M be the foot of the perpendicular drawn from B to the line joining O and A.
Let M = (x, y, z)
OM has direction ratios x - 0, y - 0, z - 0 = x, y, z
OA has direction ratios 1 - 0, 2 - 0, 3 - 0 = 1, 2, 3
But O, M, A are collinear.
∴ `"x"/1 = "y"/2 = "z"/3 = "k"` ....(Let)
∴ x = k, y = 2k, z = 3k
∴ m = (k, 2k, 3k)
BM has direction ratios
k - 4, 2k - 5, 3k - 6
∵ BM is perpendicular to OA.
∴ (1)(k - 4) + 2(2k - 5) + 3(3k - 6) = 0
∴ k - 4 + 4k - 10 + 9k - 18 = 0
∴ 14k = 32
∴ k = `16/7`
∴ M = (k, 2k, 3k) = `(16/7, 32/7, 48/7)`
Notes
The answer in the textbook is incorrect.
APPEARS IN
संबंधित प्रश्न
Find two unit vectors each of which is perpendicular to both `baru` and `barv` where `baru = 2hati + hatj - 2hatk`, `barv = hati + 2hatj - 2hatk`.
Find the values of c so that for all real x, the vectors `"xc"hat"i" - 6hat"j" + 3hat"k"` and `"x"hat"i" + 2hat"j" + 2"cx"hat"k"` make an obtuse angle.
Show that the sum of the length of projections of `"p"hat"i" + "q"hat"j" + "r"hat"k"` on the coordinate axes, where p = 2, q = 3 and r = 4 is 9.
Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular.
If `hat"p", hat"q"` and `hat"r"` are unit vectors `hat"p"+hat "r" = hat "q"`, find `hat"p".hat"q".`
If `bar"p", bar"q"` and `bar"r"` are unit vectors, find `bar"p".bar"r".`
If a line makes angles 90°, 135°, 45° with the X-, Y- and Z-axes respectively, then find its direction cosines.
The direction ratios of `bar"AB"` are −2, 2, 1. If A = (4, 1, 5) and l(AB) = 6 units, find B.
If `bar"a" = 2hat"i" + 3hat"j" - hat"k"`, `bar"b" = hat"i" - 4hat"j" + 2hat"k"`, find `(bar"a" + bar"b") xx (bar"a" - bar"b")`
Find a unit vector perpendicular to the vectors `hat"j" + 2hat"k"` and `hat"i" + hat"j"`.
If `bar"a".bar"b" = sqrt3` and `bar"a" xx bar"b" = 2hat"i" + hat"j" + 2hat"k"`, find the angle between `bar"a"` and `bar"b"`.
If `bar"a" = 2hat"i" + hat"j" - 3hat"k"` and `bar"b" = hat"i" - 2hat"j" + hat"k"`, find a vector of magnitude 5 perpendicular to both `bar"a"` and `bar"b"`.
Show that vector area of a parallelogram ABCD is `1/2 (bar"AC" xx bar"BD")` where AC and BD are its diagonals.
Find the area of parallelogram whose diagonals are determined by the vectors `bar"a" = 3hat"i" - hat"j" - 2hat"k"` and `bar"b" = - hat"i" + 3hat"j" - 3hat"k"`.
Find `bar"a"` if `bar"a" xx hat"i" + 2bar"a" - 5hat"j" = bar"0"`
If `|bar"a".bar"b"| = |bar"a" xx bar"b"|` and `bar"a".bar"b" < 0`, then find the angle between `bar"a" "and" bar"b"`.
Prove, by vector method, that sin (α + β) = sin α . cos β + cos α . sin β
Find the direction ratios of a vector perpendicular to the two lines whose direction ratios are - 2, 1, - 1 and - 3, - 4, 1
Prove that the two vectors whose direction cosines are given by relations al + bm + cn = 0 and fmn + gnl + hlm = 0 are perpendicular, if `"f"/"a" + "g"/"b" + "h"/"c" = 0`
The value of `hat"i"*(hat"j" xx hat"k") + hat"j"*(hat"i" xx hat"k") + hat"k"*(hat"i" xx hat"j")`.
Find the direction ratios of a vector perpendicular to the two lines whose direction ratios are 1, 3, 2 and –1, 1, 2
The area of triangle ABC in which c = 8 , b = 3, ∠A = 60° is ______
If the vectors `ahat("i")+hat("j")+hat("k"), hat("i")+bhat("j")+hat("k")` and `hat("i")+hat("j")+chat("k")` are coplanar (a ≠ b ≠ c ≠ 1), then the value of abc - (a + b + c) = ______.
If `vec"a" = hat"i" + hat"j" + hat"k"` and `vec"c" = hat"j" - hat"k"`. find a vector `vec"b"` satisfying `vec"a" xx vec"b" = vec"c"` and `vec"a"·vec"b"` = 3.
If `veca, vecb, vecc` are vectors such that `[(veca, vecb, vecc)]` = 4, then `[(veca xx vecb, vecb xx vecc, vecc xx veca)]` = ______.
Find two unit vectors each of which is perpendicular to both
`baru "and" barv, "where" baru = 2hati + hatj - 2hatk, barv = hati + 2hatj - 2hatk`
Find two unit vectors each of which is perpendicular to both `baru and barv, where baru = 2hati + hatj - 2hatk, barv = hati + 2hatj - 2hatk`
If a vector has direction angles 45° and 60° find the third direction angle.
Find the direction ratios of a line perpendicular to both the lines whose direction ratios are 3, –2, 1 and 2, 4, –2
Find two unit vectors each of which is perpendicular to both `baru and barv`, where `baru = 2hati + hatj - 2hatk, barv = hati + 2hatj - 2hatk`
Find two unit vectors each of which is perpendicular to both `baru and barv, "where" baru = 2hati + hatj - 2hatk, barv = hati + 2hatj - 2hatk`
If a vector has direction angles 45ºand 60º find the third direction angle.
Find two unit vectors each of which is perpendicular to both `baru and barv,` where `baru = 2hati + hatj - 2hatk, barv = hati + 2hatj - 2hatk`
