Advertisements
Advertisements
प्रश्न
If A(1, 2, 3) and B(4, 5, 6) are two points, then find the foot of the perpendicular from the point B to the line joining the origin and the point A.
उत्तर
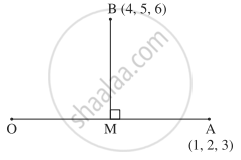
Let M be the foot of the perpendicular drawn from B to the line joining O and A.
Let M = (x, y, z)
OM has direction ratios x - 0, y - 0, z - 0 = x, y, z
OA has direction ratios 1 - 0, 2 - 0, 3 - 0 = 1, 2, 3
But O, M, A are collinear.
∴ `"x"/1 = "y"/2 = "z"/3 = "k"` ....(Let)
∴ x = k, y = 2k, z = 3k
∴ m = (k, 2k, 3k)
BM has direction ratios
k - 4, 2k - 5, 3k - 6
∵ BM is perpendicular to OA.
∴ (1)(k - 4) + 2(2k - 5) + 3(3k - 6) = 0
∴ k - 4 + 4k - 10 + 9k - 18 = 0
∴ 14k = 32
∴ k = `16/7`
∴ M = (k, 2k, 3k) = `(16/7, 32/7, 48/7)`
Notes
The answer in the textbook is incorrect.
APPEARS IN
संबंधित प्रश्न
Find the values of c so that for all real x, the vectors `"xc"hat"i" - 6hat"j" + 3hat"k"` and `"x"hat"i" + 2hat"j" + 2"cx"hat"k"` make an obtuse angle.
Find the angle P of the triangle whose vertices are P(0, - 1, - 2), Q(3, 1, 4) and R(5, 7, 1).
If `hat"p", hat"q"` and `hat"r"` are unit vectors `hat"p"+hat "r" = hat "q"`, find `hat"p".hat"q".`
If a line makes angles 90°, 135°, 45° with the X-, Y- and Z-axes respectively, then find its direction cosines.
The direction ratios of `bar"AB"` are −2, 2, 1. If A = (4, 1, 5) and l(AB) = 6 units, find B.
If `bar"a" = 2hat"i" + 3hat"j" - hat"k"`, `bar"b" = hat"i" - 4hat"j" + 2hat"k"`, find `(bar"a" + bar"b") xx (bar"a" - bar"b")`
If `bar"a" = 2hat"i" + hat"j" - 3hat"k"` and `bar"b" = hat"i" - 2hat"j" + hat"k"`, find a vector of magnitude 5 perpendicular to both `bar"a"` and `bar"b"`.
Find `bar"u".bar"v"` if `|bar"u"| = 2, |bar"v"| = 5, |bar"u" xx bar"v"| = 8`
Find `|bar"u" xx bar"v"|` if `|bar"u"| = 10, |bar"v"| = 2, bar"u".bar"v" = 12`
If `bar"a" = hat"i" - 2hat"j" + 3hat"k"` , `bar"b" = 4hat"i" - 3hat"j" + hat"k"` , `bar"c" = hat"i" - hat"j" + 2hat"k"` verify that `bar"a"xx(bar"b" + bar"c") = bar"a" xx bar"b" + bar"a" xx bar"c"`
Find the area of the parallelogram whose adjacent sides are `bar"a" = 2hat"i" - 2hat"j" + hat"k"` and `bar"b" = hat"i" - 3hat"j" - 3hat"k"`
Find the area of parallelogram whose diagonals are determined by the vectors `bar"a" = 3hat"i" - hat"j" - 2hat"k"` and `bar"b" = - hat"i" + 3hat"j" - 3hat"k"`.
If `bar"a", bar"b", bar"c", bar"d"` are four distinct vectors such that `bar"a" xx bar"b" = bar"c" xx bar"d"` and `bar"a" xx bar"c" = bar"b" xx bar"d"` prove that `bar"a" - bar"d"` is parallel to `bar"b" - bar"c"`.
If `bar"a" = hat"i" + hat"j" + hat"k" "and" bar"c" = hat"j" - hat"k"`, find `bar"a"` vector `bar"b"` satisfying `bar"a" xx bar"b" = bar"c" "and" bar"a".bar"b" = 3`
If `|bar"a".bar"b"| = |bar"a" xx bar"b"|` and `bar"a".bar"b" < 0`, then find the angle between `bar"a" "and" bar"b"`.
Find the direction ratios of a vector perpendicular to the two lines whose direction ratios are - 2, 1, - 1 and - 3, - 4, 1
The angle θ between two non-zero vectors `bar("a")` and `bar("b")` is given by cos θ = ______
If `|bar("a")*bar("b")| = |bar("a") xx bar("b")|` and `bar("a")*bar("b") < 0`, then find the angle between `bar("a")` and `bar("b")`
If the line r = `(hat"i" - 2hat"j" + 3hat"k") + lambda(2hat"i" + hat"j" + 2hat"k")` is parallel to the plane `"r" * (3hat"i" - 2hat"j" + "m"hat"k")` = 10, then the value of m is ______.
The area of triangle ABC in which c = 8 , b = 3, ∠A = 60° is ______
Let `bar"a" = 2hat"i" + hat"j" - 2hat"k" and bar"b" = hat"i" + hat"j"`. Let `vec"c"` be a vector such that `|bar"c" - bar"a"| = 3, |(bar"a" xx bar"b") xx bar"c"|` = 3 and the angle between `vec"c" and vec"a" xx vec"b" "be" 30^circ`. Then `vec"a" * vec"c"` is equal to ______.
If `bar"a"` makes an acute angle with `bar"b", bar"r"*bar"a"` = 0 and `bar"r"xx bar"b" = bar"c" xx bar"b"`, then `bar"r"` = ______.
If `vec"a" = hat"i" + hat"j" + hat"k"` and `vec"c" = hat"j" - hat"k"`. find a vector `vec"b"` satisfying `vec"a" xx vec"b" = vec"c"` and `vec"a"·vec"b"` = 3.
If `veca, vecb, vecc` are vectors such that `[(veca, vecb, vecc)]` = 4, then `[(veca xx vecb, vecb xx vecc, vecc xx veca)]` = ______.
Find two unit vectors each of which is perpendicular to both `baru "and" barv`, where `baru =2hati + hatj - 2hatk, barv =hati + 2hatj - 2hatk `
Find two unit vectors each of which is perpendicular to both `\overline "u" and \overline "v",` where ` \overline "u" = 2hati + hatj - 2hatk, \overline "v" = hati + 2hatj - 2hatk`
Find two unit vectors each of which is perpendicular to both `baru and barv, where baru = 2hati + hatj - 2hatk, barv = hati + 2hatj - 2hatk`
Find two unit vectors each of which is perpendicular to both `baru and barv` where `baru = 2hati +hatj -2hatk, barv = hati +2hatj-2hatk`
Find two unit vectors each of which is perpendicular to both `baru and barv`, where `baru = 2hati + hatj - 2hatk, barv = hati + 2hatj - 2hatk`
If a vector has direction angles 45ºand 60º find the third direction angle.
