Advertisements
Advertisements
प्रश्न
The currents flowing in the two coils of self-inductance L1 = 16 mH and L2 = 12 mH are increasing at the same rate. If the power supplied to the two coil is equal, find the ratio of induced voltages ?
उत्तर
Induced voltage, \[V = L\frac{d I}{d t}\]
\[\frac{V_1}{V_2} = \frac{L_1}{L_2} \left( as \frac{d I}{d t} \text { is same } \right)\]
\[ \Rightarrow \frac{V_1}{V_2} = \frac{16}{12} = \frac{4}{3}\]
APPEARS IN
संबंधित प्रश्न
Obtain an expression for the self-inductance of a solenoid.
Consider a solenoid carrying supplied by a source with a constant emf containing iron core inside it. When the core is pulled out of the solenoid, the change in current will ______.
A resistance of 100 `Omega`, inductor of self-inductance`(4/pi^2)` H and a capacitor of unknown capacitance are connected in series to an a.c. source of 200 V and 50 Hz. When the current and voltage are in phase, the capacitance and power dissipated is respectively ____________.
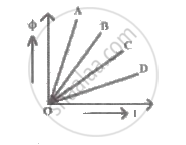
A graph of magnetic flux `(phi)` versus current (I) is shown for four inductors A, B, C and D. Larger value of self-inductance is for inductor ____________.
The frequency of γ-rays, X-rays and ultraviolet rays are a, b and c respectively. Then, ______.
Energy needed to establish an alternating current I in a coil of self-inductance L is
An inductor may store energy in
A coil of wire of a certain radius has 600 turns and a self-inductance is 108 mH. The self-inductance of a second similar coil of 500 turns will be:
An average induced emf of 0.20 V appears in a coil when the current in it is changed from 5A in one direction to 5A in the opposite direction in 0.20 sec. Find the self induction of the coil.
An air-cored solenoid, 40 cm long and of cross-sectional area 5 cm2, is tightly wound with 400 turns of copper wire and carries a steady current of 10 A. (a) Calculate the self-inductance of the solenoid. (b) Find the emf induced if the current in the solenoid decreases to zero in 0.2 s.
