Advertisements
Advertisements
प्रश्न
The experimental data for decomposition of N2O5.
\[\ce{2N2O5 -> 4NO2 + O2}\] in gas phase at 318 K are given below:
| t/s | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 |
| 102 × [N2O5]/mol L−1 | 1.63 | 1.36 | 1.14 | 0.93 | 0.78 | 0.64 | 0.53 | 0.43 | 0.35 |
- Plot [N2O5] against t.
- Find the half-life period for the reaction.
- Draw a graph between log [N2O5] and t.
- What is the rate law?
- Calculate the rate constant.
- Calculate the half-life period from k and compare it with (ii).
Advertisements
उत्तर
i.
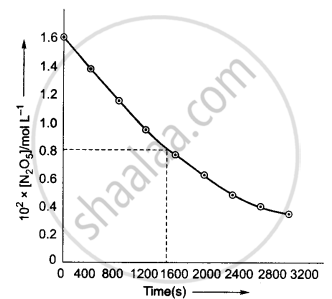
ii. Initial concentration of N2O5 = 1.63 × 10−2 M
Half of this concentration = 0.815 × 10−2 M
The time corresponding to M concentration = 1440 s
Hence, t1/2 = 1440 s
iii.
| t/s | [N2O5] × 102/mol L−1 | log [N2O5] |
| 0 | 1.63 | −1.79 |
| 400 | 1.36 | −1.87 |
| 800 | 1.14 | −1.94 |
| 1200 | 0.93 | −2.03 |
| 1600 | 0.78 | −2.11 |
| 2000 | 0.64 | −2.19 |
| 2400 | 0.53 | −2.28 |
| 2800 | 0.43 | −2.37 |
| 3200 | 0.35 | −2.46 |
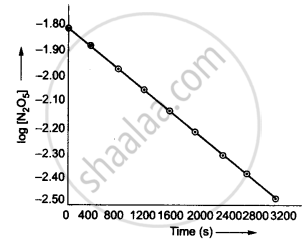
iv. The given reaction is of the first order as the plot, log [N2O5] v/s t, is a straight line. Therefore, the rate law of the reaction is:
Rate = k[N2O5]
v. For first order reaction,
log R = `- k/(2.303 t) + log R_0`
Therefore the slope of the graph drawn between log R and t will be `(-k)/2.303`
∴ The slope of the line = `-k/2.303`
= `(y_2 - y_1)/(t_2 - t_1)`
= `(-2.46 - (-1.79))/(3200 - 0)`
= `-0.67/3200`
∴ k = 4.82 × 10−4 s−1
vi. Half-life is given by,
t1/2 = `0.639/k`
= `0.693/(4.82 xx 10^-4)`
= 1.438 × 103 s
= 1438 s
This value, 1438 s, is very close to the value that was obtained from the graph.
APPEARS IN
संबंधित प्रश्न
Sucrose decomposes in acid solution to give glucose and fructose according to the first order rate law. The half life of the reaction is 3 hours. Calculate fraction of sucrose which will remain after 8 hours.
For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 90% of reaction.
A first order reaction takes 23.1 minutes for 50% completion. Calculate the time required for 75% completion of this reaction.
(log 2 = 0.301, log 3 = 0.4771, log 4 = 0.6021)
A first order reaction takes 30 minutes for 50% completion. Calculate the time required for 90% completion of this reaction.
(log 2 = 0.3010)
Which among the following reactions is an example of a zero order reaction?
a) `H_(2(g)) + I_(2(g)) -> 2HI_(g)`
b) `2H_2O_(2(l)) -> 2H_2O_(l) + O_(2(g))`
c) `C_12H_22O_(11(aq)) + H_2O_(l) -> C_6H_12O_(6(aq)) + C_6H_12O_(6(aq))`
d) `2NH_(3g)` `N(2g) + 3H_(2(g))`
A first order reaction takes 10 minutes for 25% decomposition. Calculate t1/2 for the reaction.
(Given : log 2 = 0.3010, log 3 = 0.4771, log 4 = 0.6021)
The half life period of a first order reaction is 6. 0 h . Calculate the rate constant
In a first-order reaction A → product, 80% of the given sample of compound decomposes in 40 min. What is the half-life period of the reaction?
The half life of the homogeneous gaseous reaction \[\ce{SO2Cl2 -> SO2 + Cl2}\] which obeys first order kinetics is 8.0 minutes. How long will it take for the concentration of SO2Cl2 to be reduced to 1% of the initial value?
Half life (t1/2) and completion time (T) of the zero order reaction are- (K = 0.001 mol/litre/sec and a = 1 M.)
Observe the graph shown in figure and answer the following questions:
Write the relationship between k and t1/2 (half-life period)
A sample of U238 (half-life = 4.5 × 109 years) ore is found to contain 23.8 g of U238 and 20.6 g of Pb206. The age of the ore is ______ × 109 years.
The amount of C-14 isotope in a piece of wood is found to be 1/16th of its amount present in a fresh piece of wood. The age of wood, half-life period of C-14 is 5770 years, is ______ years.
The rate of a first order reaction is 0.04 mol litre-1 s-1 at 10 minutes and 0.03 mol litre-1 sec-1 at 20 minutes after initiation. The half-life of the reaction is ______ min.
For the given first order reaction A → B the half life of the reaction is 0.3010 min. The ratio of the initial concentration of reactant to the concentration of reactant at time 2.0 min will be equal to ______. (Nearest integer)
A reaction has a half-life of 1 min. The time required for 99.9% completion of the reaction is ______ min.
(Round off to the nearest integer).
[Use: In 2 = 0.69; In 10 = 2.3]
Assertion (A): The half-life of a reaction is the time in which the concentration of the reactant is reduced to one-half of its initial concentration.
Reason (R): In first-order kinetics, when the concentration of reactant is doubled, its half-life is doubled.
The half-lives of a first-order reaction are 1.19s at 313 K and 15.45s at 293 K. Calculate the energy of activation.
Calculate the half-life of a first order reaction from the rate constant given below:
2 min−1
