Advertisements
Advertisements
प्रश्न
The experimental data for decomposition of N2O5
\[\ce{2N2O5 -> 4NO2 + O2}\] in gas phase at 318K are given below:
| t/s | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 |
| 102 × [N2O5]/mol L−1 | 1.63 | 1.36 | 1.14 | 0.93 | 0.78 | 0.64 | 0.53 | 0.43 | 0.35 |
- Plot [N2O5] against t.
- Find the half-life period for the reaction.
- Draw a graph between log [N2O5] and t.
- What is the rate law?
- Calculate the rate constant.
- Calculate the half-life period from k and compare it with (ii).
उत्तर
(i)
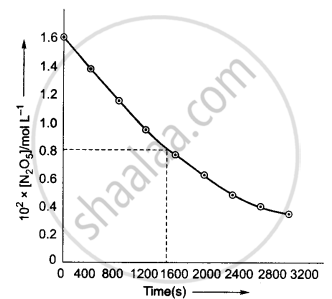
(ii) Initial concentration of N2O5 = 1.63 × 10−2 M
Half of this concentration = 0.815 × 10−2 M
The time corresponding to M concentration = 1440 s
Hence, `t_(1/2)` = 1440 s
(iii)
| t/s | [N2O5] × 102/mol L−1 | log [N2O5] |
| 0 | 1.63 | −1.79 |
| 400 | 1.36 | −1.87 |
| 800 | 1.14 | −1.94 |
| 1200 | 0.93 | −2.03 |
| 1600 | 0.78 | −2.11 |
| 2000 | 0.64 | −2.19 |
| 2400 | 0.53 | −2.28 |
| 2800 | 0.43 | −2.37 |
| 3200 | 0.35 | −2.46 |
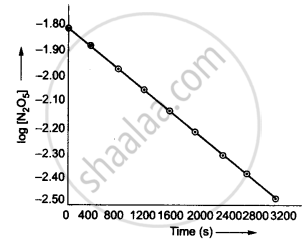
(iv) The given reaction is of the first order as the plot, log [N2O5] v/s t, is a straight line. Therefore, the rate law of the reaction is:
Rate = k[N2O5]
(v) For first order reaction,
log R = `- k/2.303t + logR_0`
Therefore the slope of the graph drawn between log R and t will be `(-k)/2.303`
∴ The slope of the line = `-k/2.303`
= `(y_2 - y_1)/(t_2 - t_1)`
= `(-2.46 - (-1.79))/(3200 - 0)`
= `-0.67/3200`
∴ k = 4.82 × 10−4 s−1
(vi) Half-life is given by,
`t_(1/2) = 0.639/k`
= `0.693/(4.82xx10^(-4))`
= 1.438 × 103 s
= 1438 s
This value, 1438 s, is very close to the value that was obtained from the graph.
APPEARS IN
संबंधित प्रश्न
Sucrose decomposes in acid solution to give glucose and fructose according to the first order rate law. The half life of the reaction is 3 hours. Calculate fraction of sucrose which will remain after 8 hours.
A first order reaction takes 23.1 minutes for 50% completion. Calculate the time required for 75% completion of this reaction.
(log 2 = 0.301, log 3 = 0.4771, log 4 = 0.6021)
A first order reaction takes 30 minutes for 50% completion. Calculate the time required for 90% completion of this reaction.
(log 2 = 0.3010)
The half-life for radioactive decay of 14C is 5730 years. An archaeological artifact containing wood had only 80% of the 14C found in a living tree. Estimate the age of the sample.
During nuclear explosion, one of the products is 90Sr with half-life of 28.1 years. If 1μg of 90Sr was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically.
The half-life period of zero order reaction A → product is given by
(a) `([A]_0)/k`
(b) `0.693/k`
(c) `[A]_0/(2k)`
(d) `(2[A]_0)/k`
A first order reaction takes 10 minutes for 25% decomposition. Calculate t1/2 for the reaction.
(Given : log 2 = 0.3010, log 3 = 0.4771, log 4 = 0.6021)
The half life period of a radioactive element is 140 days. After 560 days, 1 g of element will be reduced to
Show that for a first order reaction half life is independent of initial concentration.
The half life of the homogeneous gaseous reaction \[\ce{SO2Cl2 -> SO2 + Cl2}\] which obeys first order kinetics is 8.0 minutes. How long will it take for the concentration of SO2Cl2 to be reduced to 1% of the initial value?
Read the passage given below and answer the following question.
|
Are there nuclear reactions going on in our bodies? There are nuclear reactions constantly occurring in our bodies, but there are very few of them compared to the chemical reactions, and they do not affect our bodies much. All of the physical processes that take place to keep a human body running are chemical processes. Nuclear reactions can lead to chemical damage, which the body may notice and try to fix. The nuclear reaction occurring in our bodies is radioactive decay. This is the change of a less stable nucleus to a more stable nucleus. Every atom has either a stable nucleus or an unstable nucleus, depending on how big it is and on the ratio of protons to neutrons. The ratio of neutrons to protons in a stable nucleus is thus around 1 : 1 for small nuclei (Z < 20). Nuclei with too many neutrons, too few neutrons, or that are simply too big are unstable. They eventually transform to a stable form through radioactive decay. Wherever there are atoms with unstable nuclei (radioactive atoms), there are nuclear reactions occurring naturally. The interesting thing is that there are small amounts of radioactive atoms everywhere: in your chair, in the ground, in the food you eat, and yes, in your body. The most common natural radioactive isotopes in humans are carbon-14 and potassium-40. Chemically, these isotopes behave exactly like stable carbon and potassium. For this reason, the body uses carbon-14 and potassium-40 just like it does normal carbon and potassium; building them into the different parts of the cells, without knowing that they are radioactive. In time, carbon-14 atoms decay to stable nitrogen atoms and potassium-40 atoms decay to stable calcium atoms. Chemicals in the body that relied on having a carbon-14 atom or potassium-40 atom in a certain spot will suddenly have a nitrogen or calcium atom. Such a change damages the chemical. Normally, such changes are so rare, that the body can repair the damage or filter away the damaged chemicals. The natural occurrence of carbon-14 decay in the body is the core principle behind carbon dating. As long as a person is alive and still eating, every carbon-14 atom that decays into a nitrogen atom is replaced on average with a new carbon-14 atom. But once a person dies, he stops replacing the decaying carbon-14 atoms. Slowly the carbon-14 atoms decay to nitrogen without being replaced, so that there is less and less carbon-14 in a dead body. The rate at which carbon-14 decays is constant and follows first order kinetics. It has a half-life of nearly 6000 years, so by measuring the relative amount of carbon-14 in a bone, archeologists can calculate when the person died. All living organisms consume carbon, so carbon dating can be used to date any living organism, and any object made from a living organism. Bones, wood, leather, and even paper can be accurately dated, as long as they first existed within the last 60,000 years. This is all because of the fact that nuclear reactions naturally occur in living organisms. |
Approximately how old is a fossil with 12 g of Carbon-14 if it initially possessed 32 g of Carbon-14? (Given log 2.667 = 0.4260)
Calculate half-life period of life order reaction whose rate constant is 200 sec–1
Half life (t1/2) and completion time (T) of the zero order reaction are- (K = 0.001 mol/litre/sec and a = 1 M.)
Which radioactive isotope would have the longer half-life 15O or 19O? (Given rate constants for 15O and 19O are 5.63 × 10–3 s–1 and k = 2.38 × 10–2 s–1 respectively.)
Observe the graph shown in figure and answer the following questions:
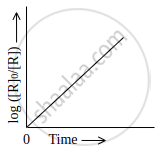
Write the relationship between k and t1/2 (half-life period)
The rate of a first order reaction is 0.04 mol litre-1 s-1 at 10 minutes and 0.03 mol litre-1 sec-1 at 20 minutes after initiation. The half-life of the reaction is ______ min.
For the given first order reaction A → B the half life of the reaction is 0.3010 min. The ratio of the initial concentration of reactant to the concentration of reactant at time 2.0 min will be equal to ______. (Nearest integer)
Assertion (A): The half-life of a reaction is the time in which the concentration of the reactant is reduced to one-half of its initial concentration.
Reason (R): In first-order kinetics, when the concentration of reactant is doubled, its half-life is doubled.
Calculate the half-life of a first order reaction from the rate constant given below:
2 min−1
