Advertisements
Advertisements
प्रश्न
The half life period of a radioactive element is 140 days. After 560 days, 1 g of element will be reduced to
पर्याय
`(1/2) "g"`
`(1/4) "g"`
`(1/8) "g"`
`(1/16) "g"`
उत्तर
`(1/16) "g"`
APPEARS IN
संबंधित प्रश्न
The integrated rate equation for first order reaction is A → products
A first order reaction takes 40 minutes for 30% decomposition. Calculate t1/2 for this reaction. (Given log 1.428 = 0.1548)
A first order reaction takes 30 minutes for 50% completion. Calculate the time required for 90% completion of this reaction.
(log 2 = 0.3010)
The experimental data for decomposition of N2O5
\[\ce{2N2O5 -> 4NO2 + O2}\] in gas phase at 318K are given below:
| t/s | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 |
| 102 × [N2O5]/mol L−1 | 1.63 | 1.36 | 1.14 | 0.93 | 0.78 | 0.64 | 0.53 | 0.43 | 0.35 |
- Plot [N2O5] against t.
- Find the half-life period for the reaction.
- Draw a graph between log [N2O5] and t.
- What is the rate law?
- Calculate the rate constant.
- Calculate the half-life period from k and compare it with (ii).
Show that for a first order reaction half life is independent of initial concentration.
Which radioactive isotope would have the longer half-life 15O or 19O? (Given rate constants for 15O and 19O are 5.63 × 10–3 s–1 and k = 2.38 × 10–2 s–1 respectively.)
Observe the graph shown in figure and answer the following questions:
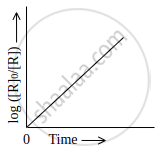
Write the relationship between k and t1/2 (half-life period)
Assertion (A): The half-life of a reaction is the time in which the concentration of the reactant is reduced to one-half of its initial concentration.
Reason (R): In first-order kinetics, when the concentration of reactant is doubled, its half-life is doubled.
Obtain a relation, `k_2/k_1 = ((t_(1/2))_2)/((t_(1/2))_1)`, where k1 and k2 are rate constants while (t1/2)1 and (t1/2)2 are half-life periods of the first order reaction at temperatures T1 and T2 respectively. Write the relation for activation energy.
Show that the half-life of zero order reaction is `t_(1/2) = ([A]_0)/(2k)`.
