Advertisements
Advertisements
प्रश्न
The given figure shows a solid formed of a solid cube of side 40 cm and a solid cylinder of radius 20 cm and height 50 cm attached to the cube as shown.
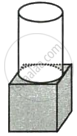
Find the volume and the total surface area of the whole solid. [Take π = 3.14].
उत्तर
Edge of a cube = I = 40 cm
∴ Volume of a cube = I3 = (40)3 = 64000 cm3
Radius of a solid cylinder = r = 20 cm
Height of a solid cylinder = h = 50 cm
∴ Volume of cylinder = πr2h
= 3.14 × 20 × 20 × 50
= 62800 cm3
∴ Volume of whole solid = Volume of cube + Volume of cylinder
= (64000 + 62800) cm3
= 126800 cm3
Total surface area of the whole solid
= Total surface area of a cube + Curved surface area of a cylinder
= 6l2 + 2πrh
= 6 × (40)2 + 2 × 3.14 × 20 × 50
= 6 × 1600 + 6280
= 9600 + 6280
= 15880 cm2
APPEARS IN
संबंधित प्रश्न
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboids are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see the following figure). Use [π = `22/7`]

Metal spheres each of radius 2cm are packed into a rectangular box of internal dimension 16cm x 8cm x 8cm when 16 spheres are packed the box is filled with preservative liquid. Find volume of this liquid?
The volume of a hemisphere is 2425`1/2cm^3`cm. Find its curved surface area?
A right circular cylinder having diameter 12 cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
The sum of the radius of the base and the height of a solid cylinder is 37 metres. If the total surface area of the cylinder be 1628 sq metres, then find its volume.
A hemisphere of lead of radius 6 cm is cast into a right circular cone of height 75 cm. Find the radius of the base of the cone.
A metallic solid right circular cone is of height 84 cm and the radius of its base is 21 cm. It is melted and recast into a solid sphere. Find the
diameter of the sphere.
How many bags of grain can be stored in a cuboidal granary (8 m × 6 m × 3 m), if each bag occupies a space of 0.64 m3?
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that `1/8` space of the cube remains unfilled. Then the number of marbles that the cube can accomodate is ______.
A rectangular water tank of base 11 m × 6 m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
