Question

The height of a solid cone is 12 cm and the area of the circular base is 64 πcm². A plane parallel to the base of the cone cuts through the cone 9 cm above the vertex of the cone, the areas of the base of the new cone so formed is ______.

विकल्प

• 9 πcm²

• 16 πcm²

•  25 πcm²

•  36 πcm² 

Answer 1

If a cone is cut into two parts by a plane parallel to the base, the portion that contains the base is called the frustum of a cone

 

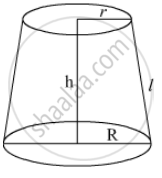
Let ‘r’ be the top radius

‘R’ be the radius of the base

‘h’ be the height of the frustum

‘l’ be the slant height of the frustum.

‘H’ be the height of the complete cone from which the frustum is cut

Then from similar triangles we can write the following relationship

`r/R =(H-h)/H`

Here it is given that the area of the base is 64π cm².

The area of the base with a base radius of ‘r’ is given by the formula

Area of base = πr²

Substituting the known values in this equation we get

64 π = πr²

r² = 64

r = 8

Hence the radius of the base of the original cone is 8 cm.

So, now let the plane cut the cone parallel to the base at 9 cm from the vertex.

Based on this we get the values as

R = 8

H = 12

H – h = 9

Substituting these values in the relationship mentioned earlier

`r/8 = 9/12`

` r = ((8)(9))/12`

r = 6

Hence the radius of the new conical part that has been formed is 6 cm.

And the area of this base of this conical part would be

Area of the base = πr²

= 36π