Advertisements
Advertisements
प्रश्न
The length of the diagonals of a cube is 8√3 cm.
Find its:
(i) edge
(ii) total surface area
(iii) Volume
उत्तर
(i) Length of diagonal of a cube = `8sqrt(3)` cm
Length of edge = `(8sqrt(3))/sqrt(3)` = 8 cm
(ii) Total surface area = 6a2 = 6 x 82 = 6 x 64 cm2 = 384 cm2
(iii) Volume = a3 = (8)3= 512 cm3
APPEARS IN
संबंधित प्रश्न
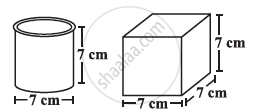
Describe how the two figures at the right are alike and how they are different. Which box has larger lateral surface area?
If each edge of a cube is doubled, how many times will its volume increase?
Find the volume of a cube whose side is 1.5 dm .
Find the volume in cubic decimetre of the cube whose side is 75 cm.
Fill in the blank in the following so as to make the statement true:
1 m3 = .........cm3
Cubes A, B, C having edges 18 cm, 24 cm and 30 cm respectively are melted and moulded into a new cube D. Find the edge of the bigger cube D.
The edges of three cubes of metal are 3 cm, 4 cm, and 5 cm. They are melted and formed into a single cube. Find the edge of the new cube.
The edges of three solid cubes are 6 cm, 8 cm, and 10 cm. These cubes are melted and recast into a single cube. Find the edge of the resulting cube.
A solid cube of side 12 cm is cut into 8 identical cubes. What will be the side of the new cube? Also, find the ratio between the surface area of the original cube and the total surface area of all the small cubes formed.
If the total surface area of a cube is 2400 cm2 then, find its lateral surface area
