Advertisements
Advertisements
प्रश्न
A cube of edge 6 cm and a cuboid with dimensions 4 cm x x cm x 15 cm are equal in volume. Find:
(i) the value of x.
(ii) the total surface area of the cuboid.
(iii) the total surface area of the cube.
(iv) which of these two has a greater surface and by how much?
उत्तर
Edge of a cube = 6 cm
Volume = a3 = (6)3 = 216 cm3
Dimensions of a cuboid = 4 cm x x cm x 15 cm
Volume = 60x cm3
The volume of both is equal
(i) ∴ `60x = 216 ⇒ x = 216/60 = 36/10`
∴ x = 3.6 cm
(ii) Total surface area of cuboid
= 2[lb + bh + hl]
= `2[4 xx 3.6 + 3.6 xx 15 + 15 xx 4]` cm2
= 2[14.4 + 54.0 + 60] cm2
= `128.4 xx 2 = 256.8` cm2
(iii) Total surface area of cube
= `6a^2 = 6(6)^2 = 6 xx 36 = 216` cm2
(iv) Difference of surface areas = 256.8 - 216
= 40.8 cm2
∴ Surface area of cuboid is greater
APPEARS IN
संबंधित प्रश्न
A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high. How much of tape is needed for all the 12 edges?
Hameed has built a cubical water tank with lid for his house, with each other edge 1 .5 m long. He gets the outer surface of the tank excluding the base, covered with square tiles of side 25 cm. Find how much he would spend for the tiles, if the cost of tiles is Rs. 360 per dozen.
The dimensions of a room are 12.5 m by 9 m by 7 m. There are 2 doors and 4 windows in the room; each door measures 2.5 m by 1 .2 m and each window 1 .5 m by I m. Find the cost of painting the walls at Rs. 3.50 per square metre.
Find the volume of a cuboid whose length = 15 cm, breadth = 2.5 dm, height = 8 cm.
Find the volume in cubic metre (cu. m) of the cuboid whose dimensions is length = 10 m, breadth = 25 dm, height = 50 cm.
A swimming pool is 250 m long and 130 m wide. 3250 cubic metres of water is pumped into it. Find the rise in the level of water.
Find the surface area of a cuboid whose length = 6 dm, breadth = 8 dm, height = 10 dm.
Show that the product of the areas of the floor and two adjacent walls of a cuboid is the square of its volume.
The breadth of a room is twice its height, one half of its length and the volume of the room is 512 cu. dm. Find its dimensions.
Three cubes of metal whose edges are in the ratio 3 : 4 : 5 are melted down in to a single cube whose diagonal is 12 `sqrt(3)` cm. Find the edges of three cubes.
The volume of a cube whose surface area is 96 cm2, is
Three cubes of each side 4 cm are joined end to end. Find the surface area of the resulting cuboid.
If each edge of a cube is increased by 50%, the percentage increase in its surface area is
If A1, A2, and A3 denote the areas of three adjacent faces of a cuboid, then its volume is
Find the volume and the total surface area of a cuboid, whose :
length = 15 cm, breadth = 10 cm and height = 8 cm.
The internal length, breadth, and height of a closed box are 1 m, 80 cm, and 25 cm. respectively. If its sides are made of 2.5 cm thick wood; find :
(i) the capacity of the box
(ii) the volume of wood used to make the box.
Find the capacity of a cylindrical container with an internal diameter of 28 cm and a height of 20 cm.
A cylindrical pillar has a radius of 21 cm and a height of 4 m. Find:
- The curved surface area of the pillar.
- cost of polishing 36 such cylindrical pillars at the rate of ₹12 per m2.
If radii of two cylinders are in the ratio 4 : 3 and their heights are in the ratio 5: 6, find the ratio of their curved surfaces.
In a building, there are 24 cylindrical pillars. For each pillar, the radius is 28 m, and the height is 4 m. Find the total cost of painting the curved surface area of the pillars at the rate of ₹ 8 per m2.
If the edge of a cube is 8 cm long, find its total surface area.
Find the volume of a cuboid whose diagonal is `3sqrt(29)"cm"` when its length, breadth and height are in the ratio 2 : 3 : 4.
The length breadth and height of a cuboid are in the ratio of 3 : 3 : 4. Find its volume in m3 if its diagonal is `5sqrt(34)"cm"`.
A room is 5m long, 2m broad and 4m high. Calculate the number of persons it can accommodate if each person needs 0.16m3 of air.
Three identical cubes of side 4 cm are joined end to end. Find the total surface area and lateral surface area of the new resulting cuboid
Opposite faces of a cuboid are ______ in area.
Find the length of the largest pole that can be placed in a room of dimensions 12 m × 4 m × 3 m.
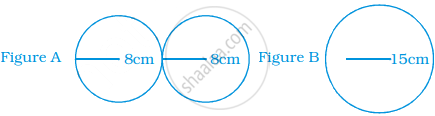
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?