Advertisements
Advertisements
प्रश्न
Find the volume in cubic metre (cu. m) of the cuboid whose dimensions is length = 10 m, breadth = 25 dm, height = 50 cm.
उत्तर
Length = 10 m
Breadth = 25 dm
\[ = \frac{25}{10}m ( \because 10 dm = 1m)\]
\[ = 2 . 5 m\]
\[\text { Height } = 25 cm = \frac{25}{100}m = 0 . 25 m\]
\[ \therefore\text { Volume of the cuboid = length } \times \text { breadth } \times\text { height }\]
\[ = 10 \times 2 . 5 \times 0 . 25\]
\[ = 6 . 25 m^3\]
APPEARS IN
संबंधित प्रश्न
Find the lateral surface area and total surface area of a cuboid of length 80 cm, breadth 40 cm and height 20 cm.
Each edge of a cube is increased by 50%. Find the percentage increase in the surface area of the cube.
The paint in a certain container is sufficient to paint on area equal to 9.375 m2. How manybricks of dimension 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?
A tank is 8 m long, 6 m broad and 2 m high. How much water can it contain?
A swimming pool is 20 m long 15 m wide and 3 m deep. Find the cost of repairing the floor and wall at the rate of Rs 25 per square metre.
The breadth and height of a rectangular solid are 1.20 m and 80 cm respectively. If the volume of the cuboid is 1.92 m3; find its length.
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of ₹ 10 per m2 is ₹ 15,000, find the height of the hall.
All six faces of a cuboid are ______ in shape and of ______ area.
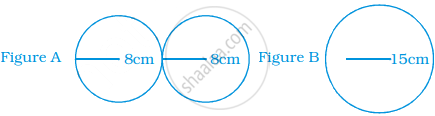
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?