Advertisements
Advertisements
प्रश्न
Find the volume in cubic metre (cu. m) of the cuboid whose dimensions is length = 10 m, breadth = 25 dm, height = 50 cm.
उत्तर
Length = 10 m
Breadth = 25 dm
\[ = \frac{25}{10}m ( \because 10 dm = 1m)\]
\[ = 2 . 5 m\]
\[\text { Height } = 25 cm = \frac{25}{100}m = 0 . 25 m\]
\[ \therefore\text { Volume of the cuboid = length } \times \text { breadth } \times\text { height }\]
\[ = 10 \times 2 . 5 \times 0 . 25\]
\[ = 6 . 25 m^3\]
APPEARS IN
संबंधित प्रश्न
Water is pouring into a cubiodal reservoir at the rate of 60 litres per minute. If the volume of the reservoir is 108 m3, find the number of hours it will take to fill the reservoir.
Find the ratio of the total surface area and lateral surface area of a cube.
Each edge of a cube is increased by 50%. Find the percentage increase in the surface area of the cube.
A water tank is 3 m long, 2 m broad and 1 m deep. How many litres of water can it hold?
The central hall of a school is 80 m long and 8 m high. It has 10 doors each of size 3 m × 1.5 m and 10 windows each of size 1.5 m × 1 m. If the cost of white-washing the walls of the hall at the rate of Rs 1.20 per m2 is Rs 2385.60, fidn the breadth of the hall.
A cuboid has total surface area of 372 cm2 and its lateral surface area is 180 cm2, find the area of its base.
The area of the floor of a room is 15 m2. If its height is 4 m, then the volume of the air contained in the room is
A closed box is cuboid in shape with length = 40 cm, breadth = 30 cm and height = 50 cm. It is made of a thin metal sheet. Find the cost of metal sheet required to make 20 such boxes, if 1 m2 of metal sheet costs Rs. 45.
The length breadth and height of a cuboid are in the ratio of 3 : 3 : 4. Find its volume in m3 if its diagonal is `5sqrt(34)"cm"`.
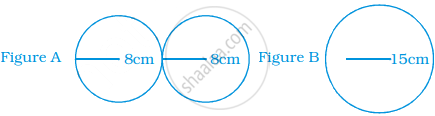
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?