Advertisements
Advertisements
प्रश्न
The sum of the heights and the radius of a solid cylinder is 35 cm and its total surface area is 3080 cm2, find the volume of the cylinder.
उत्तर
Let r and h be the radius and height of a solid cylinder
Then, r + h = 35 cm
Total surface area of a cylinder = 3080 cm2
`=>` 2πr(h + r) = 3080
`=> 2 xx 22/7 xx r xx 35 = 3080`
`=>` 2 × 22 × r × 5 = 3080
`=> r = 3080/(2 xx 22 xx 5) = 14 cm`
`=>` h = 35 – r
= 35 – 14
= 21 cm
∴ Volume of cylinder = πr2h
= `22/7 xx 14 xx 14 xx 21`
= 12936 cm3
APPEARS IN
संबंधित प्रश्न
A soft drink is available in two packs − (i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and (ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
`["Assume "pi=22/7]`
A cylindrical can, whose base is horizontal and of radius 3.5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate:
- the total surface area of the can in contact with water when the sphere is in it;
- the depth of water in the can before the sphere was put into the can.
Find the volume of the largest cylinder formed when a rectangular piece of paper 44 cm by 33 cm is rolled along its :
- shorter side.
- longer side.
The total surface area of a hollow cylinder, which is open from both the sides, is 3575 cm2; area of its base ring is 357.5 cm2 and its height is 14 cm. Find the thickness of the cylinder.
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate: the total area of the internal surface, excluding the base.
A rectangular paper of width 14 cm is rolled along its width and a cylinder of radius 20 cm is formed. Find the volume of the cylinder. (Take `22/7` for π)

A small village, having a population of 5000, requires 75 litres of water per head per day. The village has got an overhead tank of measurement 40 m × 25 m × 15 m. For how many days will the water of this tank last?
Volume of a cylinder with radius h and height r is ______.
Two cylinders of same volume have their radii in the ratio 1 : 6, then ratio of their heights is ______.
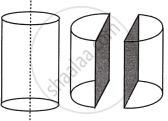
A solid metallic cylinder is cut into two identical halves along its height (as shown in the diagram). The diameter of the cylinder is 7 cm and the height is 10 cm.
Find:
- The total surface area (both the halves).
- The total cost of painting the two halves at the rate of ₹ 30 per cm2 `("Use" π = 22/7)`.