Advertisements
Advertisements
प्रश्न
The two opposite vertices of a square are (− 1, 2) and (3, 2). Find the coordinates of the other two vertices.
उत्तर

Let ABCD be a square having (−1, 2) and (3, 2) as vertices A and C respectively. Let (x, y), (x1, y1) be the coordinate of vertex B and D respectively.
We know that the sides of a square are equal to each other.
∴ AB = BC
`=>sqrt((x+1)^2 + (y-2)^2) = sqrt((x-3)^2 + (y-2)^2)`
=>x2 + 2x + 1 + y2 -4y + 4 = x2 + 9 -6x + y2 + 4 - 4y
⇒ 8x = 8
⇒ x = 1
We know that in a square, all interior angles are of 90°.
In ΔABC,
AB2 + BC2 = AC2
`=> (sqrt(((1+1)^2)+(y-2)^2))^2 + (sqrt(((1-3)^2)+(y-2)^2))^2 = (sqrt((3+1)^2+(2-2)^2))^2`
⇒ 4 + y2 + 4 − 4y + 4 + y2 − 4y + 4 =16
⇒ 2y2 + 16 − 8 y =16
⇒ 2y2 − 8 y = 0
⇒ y (y − 4) = 0
⇒ y = 0 or 4
We know that in a square, the diagonals are of equal length and bisect each other at 90°. Let O be the mid-point of AC. Therefore, it will also be the mid-point of BD
Coordinate of point O = ((-1+3)/2, (2+2)/2)
`((1+x_1)/2, (y+ y_1)/2) = (1,2)`
`(1+x_1)/2 = 1`
1+x1=2
x1 =1
and
` (y + y_1)/2 = 2`
⇒ y + y1 = 4
If y = 0,
y1 = 4
If y = 4,
y1 = 0
Therefore, the required coordinates are (1, 0) and (1, 4).
APPEARS IN
संबंधित प्रश्न
Find the area of the following triangle:
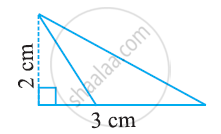
Find the area of a triangle whose vertices are
`(at_1^2,2at_1),(at_2^2,2at_2)` and `(at_3^2,2at_3)`
The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
Prove that the points (2a, 4a), (2a, 6a) and `(2a + sqrt3a, 5a)` are the vertices of an equilateral triangle.
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 5 feet | ? | 20 sq.feet |
Let ∆ = `|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`and ∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`, then ______.
Points A(–6, 10), B(–4, 6) and C(3, –8) are collinear such that AB = `2/9` AC.
The points A(2, 9), B(a, 5) and C(5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC.
Area of a triangle = `1/2` base × ______.
Triangles having the same base have equal area.
