Advertisements
Advertisements
प्रश्न
Three fair coins are tossed simultaneously. Find the probability mass function for a number of heads that occurred
उत्तर
When three coins are tossed, the sample space is
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
‘X’ is the random variable that denotes the number of heads.
∴ ‘X’ can take the values of 0, 1, 2 and 3
Sample space S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
| Values of random variable | 0 | 1 | 2 | 3 | Total |
| Number of elements in inverse image | 1 | 3 | 3 | 1 | 8 |
Probability mass function
| x | 0 | 1 | 2 | 3 |
| f(x) = P(X = x) | `1/8` | `3/8` | `3/8` | `1/8` |
or
f(x) = `{{:(1/8, "for" x = 0",", 3),(3/8, "for" x = 1",", 2):}`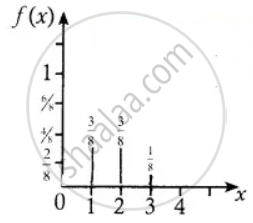
APPEARS IN
संबंधित प्रश्न
Suppose error involved in making a certain measurement is continuous r.v. X with p.d.f.
f (x) = k `(4 – x^2)`, for –2 ≤ x ≤ 2 and = 0 otherwise.
P (–0·5 < x or x > 0·5)
Given the p.d.f. of a continuous r.v. X ,
f (x) = `x^2/3` , for –1 < x < 2 and = 0 otherwise
Determine c.d.f. of X hence find P(1 < x < 2)
It is felt that error in measurement of reaction temperature (in celsius) in an experiment is a continuous r.v. with p.d.f.
f(x) = `{(x^3/(64), "for" 0 ≤ x ≤ 4),(0, "otherwise."):}`
Find probability that X is between 1 and 3..
Fill in the blank :
The values of discrete r.v. are generally obtained by _______
Solve the following problem :
Identify the random variable as discrete or continuous in each of the following. Identify its range if it is discrete.
A person on high protein diet is interested in the weight gained in a week.
c.d.f. of a discrete random variable X is
The probability distribution of a r.v. X is
| X = x | -3 | -2 | -1 | 0 | 1 |
| P(X = x) | 0.3 | 0.2 | 0.25 | 0.1 | 0.15 |
Then F (-1) = ?
Out of 100 people selected at random, 10 have common cold. If five persons selected at random from the group, then the probability that at most one person will have common cold is ______.
Suppose a discrete random variable can only take the values 0, 1, and 2. The probability mass function is defined by
`f(x) = {{:((x^2 + 1)/k"," "for" x = 0"," 1"," 2),(0"," "otherwise"):}`
Find the value of k
Choose the correct alternative:
Which of the following is a discrete random variable?
I. The number of cars crossing a particular signal in a day.
II. The number of customers in a queue to buy train tickets at a moment.
III. The time taken to complete a telephone call.
A bag contains 6 white and 4 black balls. Two balls are drawn at random. The probability that they are of the same colour is ______.
A random variable X has the following probability distribution:
| X | 1 | 2 | 3 | 4 |
| P(X) | `1/3` | `2/9` | `1/3` | `1/9` |
1hen, the mean of this distribution is ______
Two coins are tossed. Then the probability distribution of number of tails is.
The c.d.f. of a discrete r.v. X is
| X = x | -4 | -2 | -1 | 0 | 2 | 4 | 6 | 8 |
| F(x) | 0.2 | 0.4 | 0.55 | 0.6 | 0.75 | 0.80 | 0.95 | 1 |
Then P(X ≤ 4|X > -1) = ?
The p.d.f. of a continuous random variable X is
f(x) = 0.1 x, 0 < x < 5
= 0, otherwise
Then the value of P(X > 3) is ______
A coin is tossed three times. If X denotes the absolute difference between the number of heads and the number of tails then P(X = 1) = ______.
If f(x) = `k/2^x` is a probability distribution of a random variable X that can take on the values x = 0, 1, 2, 3, 4. Then, k is equal to ______.
