Advertisements
Advertisements
Question
Three fair coins are tossed simultaneously. Find the probability mass function for a number of heads that occurred
Solution
When three coins are tossed, the sample space is
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
‘X’ is the random variable that denotes the number of heads.
∴ ‘X’ can take the values of 0, 1, 2 and 3
Sample space S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
| Values of random variable | 0 | 1 | 2 | 3 | Total |
| Number of elements in inverse image | 1 | 3 | 3 | 1 | 8 |
Probability mass function
| x | 0 | 1 | 2 | 3 |
| f(x) = P(X = x) | `1/8` | `3/8` | `3/8` | `1/8` |
or
f(x) = `{{:(1/8, "for" x = 0",", 3),(3/8, "for" x = 1",", 2):}`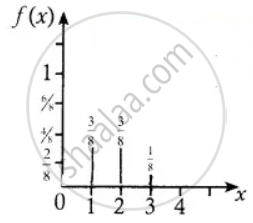
APPEARS IN
RELATED QUESTIONS
Given the p.d.f. of a continuous r.v. X , f (x) = `x^2/3` ,for –1 < x < 2 and = 0 otherwise
Determine c.d.f. of X hence find
P( x < 1)
Given the p.d.f. of a continuous r.v. X ,
f (x) = `x^2 /3` , for –1 < x < 2 and = 0 otherwise
Determine c.d.f. of X hence find P( x < –2)
Choose the correct option from the given alternative:
If the a d.r.v. X has the following probability distribution:
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P(X=x) | k | 2k | 2k | 3k | k2 | 2k2 | 7k2+k |
k =
Solve the following problem :
Identify the random variable as discrete or continuous in each of the following. Identify its range if it is discrete.
An economist is interested in knowing the number of unemployed graduates in the town with a population of 1 lakh.
The probability distribution of a r.v. X is
| X = x | -3 | -2 | -1 | 0 | 1 |
| P(X = x) | 0.3 | 0.2 | 0.25 | 0.1 | 0.15 |
Then F (-1) = ?
A coin is tossed 10 times. The probability of getting exactly six heads is ______.
Find the probability mass function and cumulative distribution function of a number of girl children in families with 4 children, assuming equal probabilities for boys and girls
The cumulative distribution function of a discrete random variable is given by
F(x) = `{{:(0, - oo < x < - 1),(0.15, - 1 ≤ x < 0),(0.35, 0 ≤ x < 1),(0.60, 1 ≤ x < 2),(0.85, 2 ≤ x < 3),(1, 3 ≤ x < oo):}`
Find the probability mass function
A random variable X has the following probability mass function.
| x | 1 | 2 | 3 | 4 | 5 |
| F(x) | k2 | 2k2 | 3k2 | 2k | 3k |
Find P(2 ≤ X < 5)
If Xis a.r.v. with c.d.f F (x) and its probability distribution is given by
| X = x | - 1.5 | -0.5 | 0.5 | 1.5 | 2.5 |
| P(X = x) | 0.05 | 0.2 | 0.15 | 0.25 | 0.35 |
then, F(1.5) - F(- 0.5) = ?
Choose the correct alternative:
Which of the following is a discrete random variable?
I. The number of cars crossing a particular signal in a day.
II. The number of customers in a queue to buy train tickets at a moment.
III. The time taken to complete a telephone call.
Choose the correct alternative:
The probability mass function of a random variable is defined as:
| x | – 2 | – 1 | 0 | 1 | 2 |
| f(x) | k | 2k | 3k | 4k | 5k |
Then E(X ) is equal to:
If A = {x ∈ R : x2 - 5 |x| + 6 = 0}, then n(A) = _____.
For a random variable X, if Var (X) = 5 and E (X2) = 21, the value of E (X) is ______
A random variable X has the following probability distribution:
| X | 1 | 2 | 3 | 4 |
| P(X) | `1/3` | `2/9` | `1/3` | `1/9` |
1hen, the mean of this distribution is ______
X is a continuous random variable with a probability density function
f(x) = `{{:(x^2/4 + k; 0 ≤ x ≤ 2),(0; "otherwise"):}`
The value of k is equal to ______
The probability distribution of a random variable X is given below.
| X = k | 0 | 1 | 2 | 3 | 4 |
| P(X = k) | 0.1 | 0.4 | 0.3 | 0.2 | 0 |
The variance of X is ______
The p.d.f. of a continuous random variable X is
f(x) = 0.1 x, 0 < x < 5
= 0, otherwise
Then the value of P(X > 3) is ______
A coin is tossed three times. If X denotes the absolute difference between the number of heads and the number of tails then P(X = 1) = ______.
For the following distribution function F(x) of a rv.x.
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| F(x) | 0.2 | 0.37 | 0.48 | 0.62 | 0.85 | 1 |
P(3 < x < 5) =
