Advertisements
Advertisements
Question
A six sided die is marked ‘1’ on one face, ‘3’ on two of its faces, and ‘5’ on remaining three faces. The die is thrown twice. If X denotes the total score in two throws, find the probability mass function
Solution
Let X be the random variable denotes the total score in two thrown of a die.
Sample space S
| I\II | 1 | 3 | 3 | 5 | 5 | 5 |
| 1 | 2 | 4 | 4 | 6 | 6 | 6 |
| 3 | 4 | 6 | 6 | 8 | 8 | 8 |
| 3 | 4 | 6 | 6 | 8 | 8 | 8 |
| 5 | 6 | 8 | 8 | 10 | 10 | 10 |
| 5 | 6 | 8 | 8 | 10 | 10 | 10 |
| 5 | 6 | 8 | 8 | 10 | 10 | 10 |
n(S) = 36
X = {2, 4, 6, 8, 10}
| Values of the random variable | 2 | 4 | 6 | 8 | 10 | Total |
| Number of elements in inverse image | 1 | 4 | 10 | 12 | 9 | 36 |
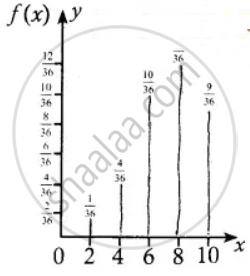
Probability mass function
| x | 2 | 4 | 6 | 8 | 10 |
| f(x) | `1/36` | `4/36` | `10/36` | `12/36` | `9/36` |
APPEARS IN
RELATED QUESTIONS
Suppose error involved in making a certain measurement is continuous r.v. X with p.d.f.
f (x) = k `(4 – x^2)`, for –2 ≤ x ≤ 2 and = 0 otherwise.
P (–0·5 < x or x > 0·5)
Given the p.d.f. of a continuous r.v. X ,
f (x) = `x^2/3` , for –1 < x < 2 and = 0 otherwise
Determine c.d.f. of X hence find P(1 < x < 2)
Given the p.d.f. of a continuous r.v. X ,
f (x) = `x^2/ 3` , for –1 < x < 2 and = 0 otherwise
Determine c.d.f. of X hence find P( X > 0)
Solve the following :
Identify the random variable as either discrete or continuous in each of the following. Write down the range of it.
An economist is interested the number of unemployed graduate in the town of population 1 lakh.
In the p.m.f. of r.v. X
| X | 1 | 2 | 3 | 4 | 5 |
| P (X) | `1/20` | `3/20` | a | 2a | `1/20` |
Find a and obtain c.d.f. of X.
It is felt that error in measurement of reaction temperature (in celsius) in an experiment is a continuous r.v. with p.d.f.
f(x) = `{(x^3/(64), "for" 0 ≤ x ≤ 4),(0, "otherwise."):}`
Verify whether f(x) is a p.d.f.
It is felt that error in measurement of reaction temperature (in celsius) in an experiment is a continuous r.v. with p.d.f.
f(x) = `{(x^3/(64), "for" 0 ≤ x ≤ 4),(0, "otherwise."):}`
Find probability that X is between 1 and 3..
Solve the following problem :
Identify the random variable as discrete or continuous in each of the following. Identify its range if it is discrete.
An economist is interested in knowing the number of unemployed graduates in the town with a population of 1 lakh.
Solve the following problem :
Identify the random variable as discrete or continuous in each of the following. Identify its range if it is discrete.
A highway safety group is interested in the speed (km/hrs) of a car at a check point.
Out of 100 people selected at random, 10 have common cold. If five persons selected at random from the group, then the probability that at most one person will have common cold is ______.
The cumulative distribution function of a discrete random variable is given by
F(x) = `{{:(0, - oo < x < - 1),(0.15, - 1 ≤ x < 0),(0.35, 0 ≤ x < 1),(0.60, 1 ≤ x < 2),(0.85, 2 ≤ x < 3),(1, 3 ≤ x < oo):}`
Find the probability mass function
The cumulative distribution function of a discrete random variable is given by
F(x) = `{{:(0, - oo < x < - 1),(0.15, - 1 ≤ x < 0),(0.35, 0 ≤ x < 1),(0.60, 1 ≤ x < 2),(0.85, 2 ≤ x < 3),(1, 3 ≤ x < oo):}`
Find P(X < 1)
If the c.d.f (cumulative distribution function) is given by F(x) = `(x - 25)/10`, then P(27 ≤ x ≤ 33) = ______.
If A = {x ∈ R : x2 - 5 |x| + 6 = 0}, then n(A) = _____.
For a random variable X, if Var (X) = 5 and E (X2) = 21, the value of E (X) is ______
A coin is tossed three times. If X denotes the absolute difference between the number of heads and the number of tails then P(X = 1) = ______.
If f(x) = `k/2^x` is a probability distribution of a random variable X that can take on the values x = 0, 1, 2, 3, 4. Then, k is equal to ______.
