Advertisements
Advertisements
प्रश्न
A six sided die is marked ‘1’ on one face, ‘3’ on two of its faces, and ‘5’ on remaining three faces. The die is thrown twice. If X denotes the total score in two throws, find the probability mass function
उत्तर
Let X be the random variable denotes the total score in two thrown of a die.
Sample space S
| I\II | 1 | 3 | 3 | 5 | 5 | 5 |
| 1 | 2 | 4 | 4 | 6 | 6 | 6 |
| 3 | 4 | 6 | 6 | 8 | 8 | 8 |
| 3 | 4 | 6 | 6 | 8 | 8 | 8 |
| 5 | 6 | 8 | 8 | 10 | 10 | 10 |
| 5 | 6 | 8 | 8 | 10 | 10 | 10 |
| 5 | 6 | 8 | 8 | 10 | 10 | 10 |
n(S) = 36
X = {2, 4, 6, 8, 10}
| Values of the random variable | 2 | 4 | 6 | 8 | 10 | Total |
| Number of elements in inverse image | 1 | 4 | 10 | 12 | 9 | 36 |
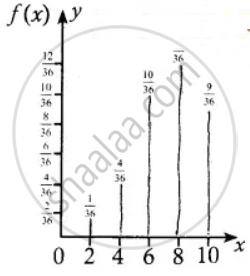
Probability mass function
| x | 2 | 4 | 6 | 8 | 10 |
| f(x) | `1/36` | `4/36` | `10/36` | `12/36` | `9/36` |
APPEARS IN
संबंधित प्रश्न
Suppose error involved in making a certain measurement is continuous r.v. X with p.d.f.
f (x) = k `(4 – x^2 )`, for –2 ≤ x ≤ 2 and = 0 otherwise.
P(x > 0)
Suppose error involved in making a certain measurement is continuous r.v. X with p.d.f.
`"f(x)" = {("k"(4 - x^2) "for –2 ≤ x ≤ 2,"),(0 "otherwise".):}`
P(–1 < x < 1)
Given the p.d.f. of a continuous r.v. X , f (x) = `x^2/3` ,for –1 < x < 2 and = 0 otherwise
Determine c.d.f. of X hence find
P( x < 1)
Given the p.d.f. of a continuous r.v. X ,
f (x) = `x^2 /3` , for –1 < x < 2 and = 0 otherwise
Determine c.d.f. of X hence find P( x < –2)
Fill in the blank :
The values of discrete r.v. are generally obtained by _______
A coin is tossed 10 times. The probability of getting exactly six heads is ______.
A random variable X has the following probability distribution:
| X = x | 0 | 1 | 2 | 3 |
| P (X = x) | `1/10` | `1/2` | `1/5` | k |
Then the value of k is
Three fair coins are tossed simultaneously. Find the probability mass function for a number of heads that occurred
Suppose a discrete random variable can only take the values 0, 1, and 2. The probability mass function is defined by
`f(x) = {{:((x^2 + 1)/k"," "for" x = 0"," 1"," 2),(0"," "otherwise"):}`
Find P(X ≥ 1)
The cumulative distribution function of a discrete random variable is given by
F(x) = `{{:(0, - oo < x < - 1),(0.15, - 1 ≤ x < 0),(0.35, 0 ≤ x < 1),(0.60, 1 ≤ x < 2),(0.85, 2 ≤ x < 3),(1, 3 ≤ x < oo):}`
Find P(X < 1)
Choose the correct alternative:
Two coins are to be flipped. The first coin will land on heads with probability 0.6, the second with Probability 0.5. Assume that the results of the flips are independent and let X equal the total number of heads that result. The value of E[X] is
A bag contains 6 white and 4 black balls. Two balls are drawn at random. The probability that they are of the same colour is ______.
If the c.d.f (cumulative distribution function) is given by F(x) = `(x - 25)/10`, then P(27 ≤ x ≤ 33) = ______.
If A = {x ∈ R : x2 - 5 |x| + 6 = 0}, then n(A) = _____.
If the probability function of a random variable X is defined by P(X = k) = a`((k + 1)/2^k)` for k - 0, 1, 2, 3, 4, 5, then the probability that X takes a prime value is ______
A random variable X has the following probability distribution:
| X | 1 | 2 | 3 | 4 |
| P(X) | `1/3` | `2/9` | `1/3` | `1/9` |
1hen, the mean of this distribution is ______
The probability distribution of a random variable X is given below.
| X = k | 0 | 1 | 2 | 3 | 4 |
| P(X = k) | 0.1 | 0.4 | 0.3 | 0.2 | 0 |
The variance of X is ______
A random variable X has the following probability distribution:
| X = xi | 1 | 2 | 3 | 4 |
| P(X = xi) | 0.2 | 0.15 | 0.3 | 0.35 |
The mean and the variance are respectively ______.
If f(x) = `k/2^x` is a probability distribution of a random variable X that can take on the values x = 0, 1, 2, 3, 4. Then, k is equal to ______.
