Advertisements
Advertisements
Question
The cumulative distribution function of a discrete random variable is given by
F(x) = `{{:(0, - oo < x < - 1),(0.15, - 1 ≤ x < 0),(0.35, 0 ≤ x < 1),(0.60, 1 ≤ x < 2),(0.85, 2 ≤ x < 3),(1, 3 ≤ x < oo):}`
Find the probability mass function
Solution
Given F(x) = `{{:(0, - oo < x < - 1),(0.15, - 1 ≤ x < 0),(0.35, 0 ≤ x < 1),(0.60, 1 ≤ x < 2),(0.85, 2 ≤ x < 3),(1, 3 ≤ x < oo):}`
The value of 'x' are –1, 0, 1, 2, 3
F(–1) = P(X = –1)
= F(–1) – F(–1)
= 0.15 – 0
= 0.15
F(0) = P(X = 0)
= F(0) – F(–1)
= 0.35 – 0.15
= 0.20
F(1) = P(X = 1)
= F(1) – F(0)
= 0.60 – 0.35 =
0.25
F(2) = P(X = 2)
= F(2) – F(1)
= 0.85 – 0.60
= 0.25
F(3) = P(X = 3)
= F(3) – F(2)
= 1 – 0.85
= 0.15
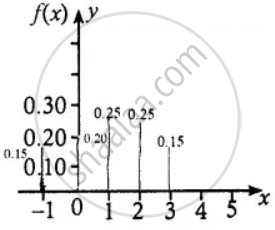
Probability mass function table
| x | –1 | 0 | 1 | 2 | 3 |
| F(x) | 0.15 | 0.20 | 0.25 | 0.25 | 0.15 |
APPEARS IN
RELATED QUESTIONS
Solve the following :
Identify the random variable as either discrete or continuous in each of the following. Write down the range of it.
An economist is interested the number of unemployed graduate in the town of population 1 lakh.
It is felt that error in measurement of reaction temperature (in celsius) in an experiment is a continuous r.v. with p.d.f.
f(x) = `{(x^3/(64), "for" 0 ≤ x ≤ 4),(0, "otherwise."):}`
Find P(0 < X ≤ 1).
Fill in the blank :
The value of continuous r.v. are generally obtained by _______
The probability distribution of a r.v. X is
| X = x | -3 | -2 | -1 | 0 | 1 |
| P(X = x) | 0.3 | 0.2 | 0.25 | 0.1 | 0.15 |
Then F (-1) = ?
Three fair coins are tossed simultaneously. Find the probability mass function for a number of heads that occurred
The cumulative distribution function of a discrete random variable is given by
F(x) = `{{:(0, - oo < x < - 1),(0.15, - 1 ≤ x < 0),(0.35, 0 ≤ x < 1),(0.60, 1 ≤ x < 2),(0.85, 2 ≤ x < 3),(1, 3 ≤ x < oo):}`
Find P(X < 1)
A random variable X has the following probability mass function.
| x | 1 | 2 | 3 | 4 | 5 |
| F(x) | k2 | 2k2 | 3k2 | 2k | 3k |
Find P(X > 3)
Choose the correct alternative:
A pair of dice numbered 1, 2, 3, 4, 5, 6 of a six-sided die and 1, 2, 3, 4 of a four-sided die is rolled and the sum is determined. Let the random variable X denote this sum. Then the number of elements in the inverse image of 7 is
A bag contains 6 white and 4 black balls. Two balls are drawn at random. The probability that they are of the same colour is ______.
If the c.d.f (cumulative distribution function) is given by F(x) = `(x - 25)/10`, then P(27 ≤ x ≤ 33) = ______.
If A = {x ∈ R : x2 - 5 |x| + 6 = 0}, then n(A) = _____.
The probability distribution of a random variable X is given below. If its mean is 4.2, then the values of a and bar respectively
| X = x | 1 | 2 | 3 | 4 | 5 | 6 |
| P(X = x) | a | a | a | b | b | 0.3 |
The probability distribution of a random variable X is given below.
| X = k | 0 | 1 | 2 | 3 | 4 |
| P(X = k) | 0.1 | 0.4 | 0.3 | 0.2 | 0 |
The variance of X is ______
A card is chosen from a well-shuffled pack of cards. The probability of getting an ace of spade or a jack of diamond is ______.
Two coins are tossed. Then the probability distribution of number of tails is.
The p.d.f. of a continuous random variable X is
f(x) = 0.1 x, 0 < x < 5
= 0, otherwise
Then the value of P(X > 3) is ______
A random variable X has the following probability distribution:
| X = xi | 1 | 2 | 3 | 4 |
| P(X = xi) | 0.2 | 0.15 | 0.3 | 0.35 |
The mean and the variance are respectively ______.
For the following distribution function F(x) of a rv.x.
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| F(x) | 0.2 | 0.37 | 0.48 | 0.62 | 0.85 | 1 |
P(3 < x < 5) =
