Advertisements
Advertisements
प्रश्न
Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is ______.
विकल्प
2 cm
3 cm
4 cm
6 cm
उत्तर
Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is 2 cm.
Explanation:
Let the diameter of each sphere be d cm.
Let r and R be the radii of the sphere and the cylinder, respectively, and h be the height of the cylinder.
As R = `"Diameter"/2.`
`"R" = 2/2 "cm" = 1 " cm"`
h = 16 cm
Therefore,
`=> 12 × 4/3xxpi"r"^3 = pi"R"^2"h"`
`=>12xx4/3"r"^3 = "R"^2"h"`
`=> 12xx4/3("d"/2)^3 = (1)^2 xx 16`
`=> 16xx"d"^3/8 = 16`
⇒ d3 = 8
⇒ d = ± 2
since d cannot of each sphere is 2 cm.
Hence, the diameter of each sphere is 2 cm.
APPEARS IN
संबंधित प्रश्न
Metal spheres each of radius 2cm are packed into a rectangular box of internal dimension 16cm x 8cm x 8cm when 16 spheres are packed the box is filled with preservative liquid. Find volume of this liquid?
A cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water. Find the value of water (i) displaced out of the cylinder (ii) left in the cylinder. (Take π 22/7)
Two cubes each of volume 125 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
Choose the correct answer of the following question:
The number of solid spheres, each of diameter 6 cm, that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm, is
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. The ratio of their volumes is ______.
A metallic cone of base radius 2.1 cm and height 8.4 cm is melted and moulded into a sphere. The radius of the sphere is
The figure shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end, PQ = 200 m; PT = 70 meters.
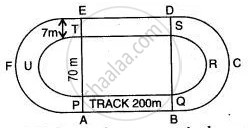
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track. (Take π = `22/7`)
The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is ______.
Find the volume of a solid hemisphere whose total surface area is 462 sq.m.
A solid is in the shape of a hemisphere of radius 7 cm, surmounted by a cone of height 4 cm. The solid is immersed completely in a cylindrical container filled with water to a certain height. If the radius of the cylinder is 14 cm, find the rise in the water level.