Advertisements
Advertisements
प्रश्न
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels 5 km/hr faster than the second train. If after 2 hours, they are 50 km apart, find the speed of each train.
उत्तर
Let take the speed of the second train to be x km/hr
Then, the speed of the first train is (x + 5) km/hr
Let O be the position of the railway station from which the two trains leave.
Distance travelled by the first train in 2 hours
= OA
= Speed × Time
= 2(x + 5) km
Distance travelled by the second train in 2 hours
= OB
= Speed × Time
= 2x km
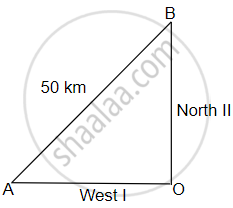
By Pythagoras Theorem, we have
(AB)2 = (OA)2 + (OB)2
`=>` (50)2 = [2(x + 5)]2 + (2x)2
`=>` 2500 = 4(x + 5)2 = 4x2
`=>` 2500 = 4(x2 + 25 + 10x) + 4x2
`=>` 8x2 + 40x – 2400 = 0
`=>` x2 + 20x – 15x – 300 = 0
`=>` (x + 20)(x – 15) = 0
`=>` x = –20 or x = 15
`=>` x = 15 ...[∵ x cannot be negative]
Hence, the speed of the second train is 15 km/hr and the speed of the first train is 20 km/hr.
APPEARS IN
संबंधित प्रश्न
The speed of an ordinary train is x km per hr and that of an express train is (x + 25) km per hr.
- Find the time taken by each train to cover 300 km.
- If the ordinary train takes 2 hrs more than the express train; calculate speed of the express train.
If the speed of a car is increased by 10 km per hr, it takes 18 minutes less to cover a distance of 36 km. Find the speed of the car.
If the speed of an aeroplane is reduced by 40 km/hr, it takes 20 minutes more to cover 1200 km. Find the speed of the aeroplane.
Some school children went on an excursion by a bus to a picnic spot at a distance of 300 km. While returning, it was raining and the bus had to reduce its speed by 5 km/hr and it took two hours longer for returning. Find the time taken to return.
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain its speed gets reduced by 10 km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be 'x' km/h, form an equation and solve it to evaluate 'x'.
An aeroplane travelled a distance of 400 km at an average speed of x km/hr. On the return journey, the speed was increased by 40 km/hr. Write down an expression for the time taken for:
- the onward journey;
- the return journey.
If the return journey took 30 minutes less than the onward journey, write down an equation in x and find its value.
A man covers a distance of 100 km, travelling with a uniform speed of x km/hr. Had the speed been 5 km/hr more it would have taken 1 hour less. Find x the original speed.
The given table shows the distance covered and the time taken by a train moving at a uniform speed along a straight track:
| Distance (in m) | 60 | 90 | y |
| Time (in sec) | 2 | x | 5 |
The values of x and y are:
A car travels a distance of 72 km at a certain average speed of x km per hour and then travels a distance of 81 km at an average speed of 6 km per hour more than its original average speed. If it takes 3 hours to complete the total journey then form a quadratic equation and solve it to find its original average speed.
The speed of train A is x km/h and speed of train B is (x – 5) km/h. How much time will each train take to cover 400 km?
