Advertisements
Advertisements
प्रश्न
Use Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R.
Draw the magnetic field lines due to a circular wire carrying current I.
उत्तर
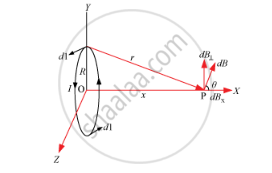
I = Current in the loop
R = Radius of the loop
X-axis = Axis of the loop
X = Distance between O and P
dl = Conducting element of the loop
According to the Biot–Savart law, the magnetic field at P is
`dB=(mu_0)/(4pi) (I|dlxxr|)/r^3`
r2 = x2 + R2
|dl × r| = rdl (Because they are perpendicular)
`:.dB=mu_0/(4pi) (Idl)/((x^2+R^2))`
dB has two components: dBx and dB⊥. dB⊥ is cancelled out and only the x-component remains.
∴ dBx= dBcos θ
`costheta= R/(x^2+R^2)^(1/2)`
`:.dB_x=(mu_0Idl)/(4pi) R/(x^2+R^2)^(3/2)`
Summation of dl over the loop is given by 2πR.
`:.B=B=B_xhati=(mu_0IR^2)/(2(x^2+R^2)^(3/2))hati`
APPEARS IN
संबंधित प्रश्न
Two identical circular coils, P and Q each of radius R, carrying currents 1 A and √3A respectively, are placed concentrically and perpendicular to each other lying in the XY and YZ planes. Find the magnitude and direction of the net magnetic field at the centre of the coils.
A steady electric current is flowing through a cylindrical conductor.
(a) The electric field at the axis of the conductor is zero.
(b) The magnetic field at the axis of the conductor is zero.
(c) The electric field in the vicinity of the conductor is zero.
(d) The magnetic field in the vicinity of the conductor is zero.
A circular loop of radius r carrying a current i is held at the centre of another circular loop of radius R(>>r) carrying a current I. The plane of the smaller loop makes an angle of 30° with that of the larger loop. If the smaller loop is held fixed in this position by applying a single force at a point on its periphery, what would be the minimum magnitude of this force?
Find the magnetic field B due to a semicircular wire of radius 10.0 cm carrying a current of 5.0 A at its centre of curvature.
A circular loop of radius 4.0 cm is placed in a horizontal plane and carries an electric current of 5.0 A in the clockwise direction as seen from above. Find the magnetic field (a) at a point 3.0 cm above the centre of the loop (b) at a point 3.0 cm below the centre of the loop.
The magnetic field at a distance r from a long wire carrying current I is 0.4 tesla. The magnetic field at a distance 2 r is ______.
A charged particle moving in a uniform magnetic field and losses 4% of its kinetic energy. The radius of curvature of its path changes by ______.
A short bar magnet has a magnetic moment of 0. 65 J T-1, then the magnitude and direction of the magnetic field produced by the magnet at a distance 8 cm from the centre of magnet on the axis is ______.
If ar and at represent radial and tangential accelerations, the motion of the particle will be uniformly circular, if:
Consider a circular current-carrying loop of radius R in the x-y plane with centre at origin. Consider the line intergral
`ℑ(L ) = |int_(-L)^L B.dl|` taken along z-axis.
- Show that ℑ(L) monotonically increases with L.
- Use an appropriate Amperian loop to show that ℑ(∞) = µ0I, where I is the current in the wire.
- Verify directly the above result.
- Suppose we replace the circular coil by a square coil of sides R carrying the same current I. What can you say about ℑ(L) and ℑ(∞)?
