Advertisements
Advertisements
प्रश्न
Find the magnetic field B due to a semicircular wire of radius 10.0 cm carrying a current of 5.0 A at its centre of curvature.
उत्तर
Given:
Magnitude of current, I = 5 A
Radius of the semi-circular wire, r = 10 cm
∴ Required magnetic field at the centre of curvature
\[B = \frac{1}{2} \times \frac{\mu_0 i}{2r}\]
\[ = {10}^{- 7} \times \frac{5}{10 \times {10}^{- 2}}\]
\[ = 5\pi \times {10}^{- 6} \]
\[ = 1 . 6 \times {10}^{- 5} \] T
APPEARS IN
संबंधित प्रश्न
Use Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R.
Draw the magnetic field lines due to a circular wire carrying current I.
Two concentric circular coils X and Y of radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A; coil Y has 25 turns and carries a current of 18 A. The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.
Two identical circular coils, P and Q each of radius R, carrying currents 1 A and √3A respectively, are placed concentrically and perpendicular to each other lying in the XY and YZ planes. Find the magnitude and direction of the net magnetic field at the centre of the coils.
At a place, the horizontal component of earth's magnetic field is B and angle of dip is 60°. What is the value of horizontal component of the earth's magnetic field at equator?
Using Biot-Savart law, deduce the expression for the magnetic field at a point (x) on the axis of a circular current carrying loop of radius R. How is the direction of the magnetic field determined at this point?
Use Biot-Savart's law to find the expression for the magnetic field due to a circular loop of radius 'r' carrying current 'I', at its centre ?
Consider the situation shown in figure. The straight wire is fixed but the loop can move under magnetic force. The loop will
A steady electric current is flowing through a cylindrical conductor.
(a) The electric field at the axis of the conductor is zero.
(b) The magnetic field at the axis of the conductor is zero.
(c) The electric field in the vicinity of the conductor is zero.
(d) The magnetic field in the vicinity of the conductor is zero.
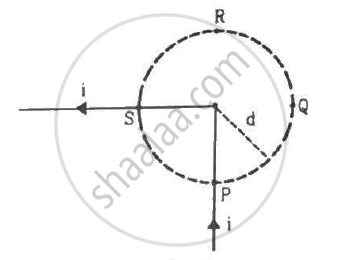
Figure shows a long wire bent at the middle to form a right angle. Show that the magnitudes of the magnetic fields at the point P, Q, R and S are equal and find this magnitude.
A circular loop of radius r carrying a current i is held at the centre of another circular loop of radius R(>>r) carrying a current I. The plane of the smaller loop makes an angle of 30° with that of the larger loop. If the smaller loop is held fixed in this position by applying a single force at a point on its periphery, what would be the minimum magnitude of this force?
A circular loop of radius r carries a current i. How should a long, straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
Which of these equations is the correct expression for force on a charge in magnetic field?
The magnetic field at a distance r from a long wire carrying current I is 0.4 tesla. The magnetic field at a distance 2 r is ______.
If we double the radius of a coil keeping the current through it unchanged, then the magnetic field at any point at a large distance from the centre becomes approximately.
Consider a circular current-carrying loop of radius R in the x-y plane with centre at origin. Consider the line intergral
`ℑ(L ) = |int_(-L)^L B.dl|` taken along z-axis.
- Show that ℑ(L) monotonically increases with L.
- Use an appropriate Amperian loop to show that ℑ(∞) = µ0I, where I is the current in the wire.
- Verify directly the above result.
- Suppose we replace the circular coil by a square coil of sides R carrying the same current I. What can you say about ℑ(L) and ℑ(∞)?
The fractional change in the magnetic field intensity at a distance 'r' from centre on the axis of the current-carrying coil of radius 'a' to the magnetic field intensity at the centre of the same coil is ______.
(Take r < a).
Two horizontal thin long parallel wires, separated by a distance r carry current I each in the opposite directions. The net magnetic field at a point midway between them will be ______.
