Advertisements
Advertisements
प्रश्न
Using Biot-Savart law, deduce the expression for the magnetic field at a point (x) on the axis of a circular current carrying loop of radius R. How is the direction of the magnetic field determined at this point?
उत्तर
Magnetic field on the axis of a circular current loop
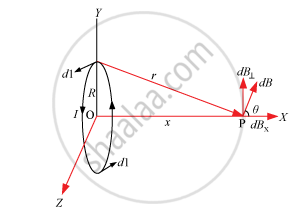
I = Current in the loop
R = Radius of the loop
X-axis = Axis of the loop
X = Distance between O and P
dl = Conducting element of the loop
According to the Biot–Savart law, the magnetic field at P is
`dB =(μ_0 I | dl xxr)/(4π r^3)`
r2 = x2 + R2
|dl × r| = rdl (Because they are perpendicular)
`dB =(μ_0 I dl )/(4π (x^2 + R^2))`
dB has two components: dBx and dB⊥. dB⊥ is cancelled out and only the x-component remains.
∴ dBx= dBcos θ
`cos θ= R/ (x^2 + R^2)^(3/2) hati`
Summation of dl over the loop is given by 2πR.
∴ `B = B= B_x hati = (μ_0 I R^2)/(2(x^2 + R^2)^(3/2)) hati `
The direction of
APPEARS IN
संबंधित प्रश्न
Use Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R.
Draw the magnetic field lines due to a circular wire carrying current I.
A circular loop is kept in that vertical plane which contains the north-south direction. It carries a current that is towards north at the topmost point. Let A be a point on the axis of the circle to the east of it and B a point on this axis to the west of it. The magnetic field due to the loop
A steady electric current is flowing through a cylindrical conductor.
(a) The electric field at the axis of the conductor is zero.
(b) The magnetic field at the axis of the conductor is zero.
(c) The electric field in the vicinity of the conductor is zero.
(d) The magnetic field in the vicinity of the conductor is zero.
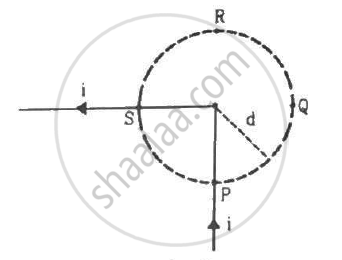
Figure shows a long wire bent at the middle to form a right angle. Show that the magnitudes of the magnetic fields at the point P, Q, R and S are equal and find this magnitude.
A circular loop of radius R carries a current I. Another circular loop of radius r(<<R) carries a current i and is placed at the centre of the larger loop. The planes of the two circles are at right angle to each other. Find the torque acting on the smaller loop.
A charge of 3.14 × 10−6 C is distributed uniformly over a circular ring of radius 20.0 cm. The ring rotates about its axis with an angular velocity of 60.0 rad s−1. Find the ratio of the electric field to the magnetic field at a point on the axis at a distance of 5.00 cm from the centre.
Which of these equations is the correct expression for force on a charge in magnetic field?
A small square loop of wire of side l is placed inside a large square loop of side L (L >> l). The loop is coplanar and their centers coincide. The mutual inductance of the system is proportional to is
The fractional change in the magnetic field intensity at a distance 'r' from centre on the axis of the current-carrying coil of radius 'a' to the magnetic field intensity at the centre of the same coil is ______.
(Take r < a).
