Advertisements
Advertisements
प्रश्न
Using Biot-Savart law, deduce the expression for the magnetic field at a point (x) on the axis of a circular current carrying loop of radius R. How is the direction of the magnetic field determined at this point?
उत्तर
Magnetic field on the axis of a circular current loop
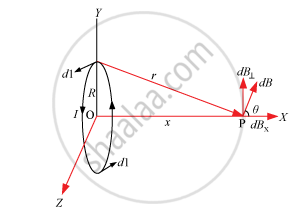
I = Current in the loop
R = Radius of the loop
X-axis = Axis of the loop
X = Distance between O and P
dl = Conducting element of the loop
According to the Biot–Savart law, the magnetic field at P is
`dB =(μ_0 I | dl xxr)/(4π r^3)`
r2 = x2 + R2
|dl × r| = rdl (Because they are perpendicular)
`dB =(μ_0 I dl )/(4π (x^2 + R^2))`
dB has two components: dBx and dB⊥. dB⊥ is cancelled out and only the x-component remains.
∴ dBx= dBcos θ
`cos θ= R/ (x^2 + R^2)^(3/2) hati`
Summation of dl over the loop is given by 2πR.
∴ `B = B= B_x hati = (μ_0 I R^2)/(2(x^2 + R^2)^(3/2)) hati `
The direction of
APPEARS IN
संबंधित प्रश्न
Derive the expression for the torque on a rectangular current carrying loop suspended in a uniform magnetic field.
Consider the situation shown in figure. The straight wire is fixed but the loop can move under magnetic force. The loop will
A circular loop of radius r carrying a current i is held at the centre of another circular loop of radius R(>>r) carrying a current I. The plane of the smaller loop makes an angle of 30° with that of the larger loop. If the smaller loop is held fixed in this position by applying a single force at a point on its periphery, what would be the minimum magnitude of this force?
Find the magnetic field B due to a semicircular wire of radius 10.0 cm carrying a current of 5.0 A at its centre of curvature.
A circular loop of radius r carries a current i. How should a long, straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
A charge of 3.14 × 10−6 C is distributed uniformly over a circular ring of radius 20.0 cm. The ring rotates about its axis with an angular velocity of 60.0 rad s−1. Find the ratio of the electric field to the magnetic field at a point on the axis at a distance of 5.00 cm from the centre.
The magnetic field at a distance r from a long wire carrying current I is 0.4 tesla. The magnetic field at a distance 2 r is ______.
A charged particle moving in a uniform magnetic field and losses 4% of its kinetic energy. The radius of curvature of its path changes by ______.
An electron is projected along the axis of a circular conductor carrying some current. Electron ______
